213/16 1) x gerçek sayısı için, 0 < x < 1 ise,
Cevap: (1,∞)
213/18 2) Her pozitif x, y gerçek sayısı için,
olduğu bilinmektedir.Pozitif x gerçek sayısı için x + 4/x toplamının en küçük değeri nedir?
Cevap: 4
214/8 3) x,y,z ∈ R için,
x.z - y.z < 0
x³ > 1 ve y² < y
ise hangisi daima doğrudur?
Cevap: 1/z < 1/x < 1/y
215/13 4)
a³ < |a| < a²
a.b < b+2
eşitsizliklerine göre b nin en geniş aralığı nedir?
Cevap: b > -1
215/14 5)
1-x < 4-2x ≤ x+1
eşitsizliğinin en geniş çözüm aralığı nedir?
Cevap: 1≤x<3
Biraz çok soru soruyorum; fakat günlük 5 soruyu geçmiyorum.Umarım sorun olmuyordur.Çözümleriniz için şimdiden teşekkürler
1
1-x
ifadesinin alabileceği değer aralığı nedir?
Cevap: (1,∞)
213/18 2) Her pozitif x, y gerçek sayısı için,
x+y
2
≥ √x.y
olduğu bilinmektedir.Pozitif x gerçek sayısı için x + 4/x toplamının en küçük değeri nedir?
Cevap: 4
214/8 3) x,y,z ∈ R için,
x.z - y.z < 0
x³ > 1 ve y² < y
ise hangisi daima doğrudur?
Cevap: 1/z < 1/x < 1/y
215/13 4)
a³ < |a| < a²
a.b < b+2
eşitsizliklerine göre b nin en geniş aralığı nedir?
Cevap: b > -1
215/14 5)
1-x < 4-2x ≤ x+1
eşitsizliğinin en geniş çözüm aralığı nedir?
Cevap: 1≤x<3
Biraz çok soru soruyorum; fakat günlük 5 soruyu geçmiyorum.Umarım sorun olmuyordur.Çözümleriniz için şimdiden teşekkürler
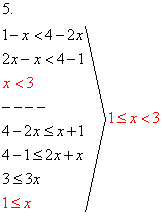
Diğer soruları çözebilecek olan yok mu? 
bilgisayarını faresi takılıp durduğu için telefondan yazıyorum, çözümler biraz fazla sözel ve kısa olabilir, anlaşılmayan yerleri sorarsanız açıklayabiliriz, şimdiden kusura bakmayın diyorum.
1.
1-x kesinlikle pozitif bir değer alacaktır ve 1 den küçüktür.
ayrıca fonksiyon verilen aralıkta sürekli olduğundan değer aralığını da örter
x 0 a giderken ifade 1 e , x 1 e giderken de ifade sonsuza gider
cevap (1, sonsuz) olur
2.
verilen kuralı (aritmetik ortalama> geometrik ortalama) kullanırsanız
(x+(4/x))/2>=(x.(4/x))^(1/2)=2
yani sıyrılan şeyin yarısı en az 2 bulunur,
sorulan ifade de en az 4 olur. (x=2 için bu değerin alındığını da söylemeliyiz)
3.
x>1 olacaktır, y pozitif olacağından sadeleştirirsek 0<y<1 elde ederiz
z parantezine alınca z.(x-y)<0 bulunur, x-y pozitif olacağından z nin de negatif olduğunu buluruz.
bundan sonrası seçeneklerden hangisinin bunlara uyduğunu bulmaya kalıyor mesela yazdığınız cevap uygun.
4.
a²>|a| olduğundan |a|>1 bulunur
ayrıca a³<a² olduğundan a negatif olur yani a<-1
sorulan ifade düzenlenirse
b>2/(a-1) bulunur (a-1 in negatif olduğuna dikkat ediniz, eşitsizliğin yönü değişir)
bu da a -1 e giderken b>-1 olur.
1.
1-x kesinlikle pozitif bir değer alacaktır ve 1 den küçüktür.
ayrıca fonksiyon verilen aralıkta sürekli olduğundan değer aralığını da örter
x 0 a giderken ifade 1 e , x 1 e giderken de ifade sonsuza gider
cevap (1, sonsuz) olur
2.
verilen kuralı (aritmetik ortalama> geometrik ortalama) kullanırsanız
(x+(4/x))/2>=(x.(4/x))^(1/2)=2
yani sıyrılan şeyin yarısı en az 2 bulunur,
sorulan ifade de en az 4 olur. (x=2 için bu değerin alındığını da söylemeliyiz)
3.
x>1 olacaktır, y pozitif olacağından sadeleştirirsek 0<y<1 elde ederiz
z parantezine alınca z.(x-y)<0 bulunur, x-y pozitif olacağından z nin de negatif olduğunu buluruz.
bundan sonrası seçeneklerden hangisinin bunlara uyduğunu bulmaya kalıyor mesela yazdığınız cevap uygun.
4.
a²>|a| olduğundan |a|>1 bulunur
ayrıca a³<a² olduğundan a negatif olur yani a<-1
sorulan ifade düzenlenirse
b>2/(a-1) bulunur (a-1 in negatif olduğuna dikkat ediniz, eşitsizliğin yönü değişir)
bu da a -1 e giderken b>-1 olur.
2 ve 5. sorunun çözümlerini anlayamadım.Acaba bilgisayarınızın faresi düzeldiyse tekrar çözebilir misiniz?Veya böyle bir imkanınız yoksa başka birisi çözebilir mi?
x + (4/x) en küçük ne olur diyor yukarıda çözülmüş zaten şu yapılmış sağ tarafın okunmasında sıkıtı var galiba
x ile 4/x sayılarının aritmetik ortalaması ≥ geometrik ortalaması olduğundan
≥ √x.4/x
x + 4/x ≥ 2√4
x + (4/x)≥4
sorulan ifade ≥ 4 ise en küçük değeri tabikide 4 olur bunuda x=2 için alır
5.sorunuzun çözümüde önce sol taraf incelenmiş sonrada sağ taraf incelenip x için gereken aralık bulunmuş çözüm gayet açık biraz daha dikkatli inceleyin başarılar...
x ile 4/x sayılarının aritmetik ortalaması ≥ geometrik ortalaması olduğundan
x + (4/x)
2
≥ √x.4/x
x + 4/x ≥ 2√4
x + (4/x)≥4
sorulan ifade ≥ 4 ise en küçük değeri tabikide 4 olur bunuda x=2 için alır
5.sorunuzun çözümüde önce sol taraf incelenmiş sonrada sağ taraf incelenip x için gereken aralık bulunmuş çözüm gayet açık biraz daha dikkatli inceleyin başarılar...
gereksizyorumcunun çözdüğu son soruyu 5. Sandım en sonda olduğu için.2 ve 4 olcaktı.Çok pardon
