(n,n-3)+(n,n-2)=56 ise n kaçtır? Bu soruda 3. dereceden denklem çıkardım, oradan şıkları deneyerek cevabın 7 olduğunu buldum ama kesin bir çözümünü arıyorum.
(10,0)+(10,1)+(10,2)+...+(10,10)=? cevap 2 üzeri 10
(19,0)+(19,1)+(19,2)+...+(19,9)=? cevap 2 üzeri 18
(10,0)+(10,1)+(10,2)+...+(10,10)=? cevap 2 üzeri 10
(19,0)+(19,1)+(19,2)+...+(19,9)=? cevap 2 üzeri 18
(10,0)+(10,1)+(10,2)+...+(10,10)=? cevap 2 üzeri 10
(19,0)+(19,1)+(19,2)+...+(19,9)=? cevap 2 üzeri 18
Bu iki soru tanım sorusudur. Konuyu bilen her kişi yapabilir uzun lafın kısası konuya bakmanı öneririm.
(19,0)+(19,1)+(19,2)+...+(19,9)=? cevap 2 üzeri 18
Bu iki soru tanım sorusudur. Konuyu bilen her kişi yapabilir uzun lafın kısası konuya bakmanı öneririm.
bu kısımları oku geç ya uzatmadan alt küme sayısı işte 0 elemanlı + 1 elemanlı +n elemanlı filan
(10,0)+(10,1)+(10,2)+...+(10,10)=? cevap 2 üzeri 10
(19,0)+(19,1)+(19,2)+...+(19,9)=? cevap 2 üzeri 18
Bu iki soru tanım sorusudur. Konuyu bilen her kişi yapabilir uzun lafın kısası konuya bakmanı öneririm.
(19,0)+(19,1)+(19,2)+...+(19,9)=? cevap 2 üzeri 18
Bu iki soru tanım sorusudur. Konuyu bilen her kişi yapabilir uzun lafın kısası konuya bakmanı öneririm.
İspat sorman güzel bir şey, birçok kişi bu kombinasyon formüllerini ezberleyip geçerler.
_____

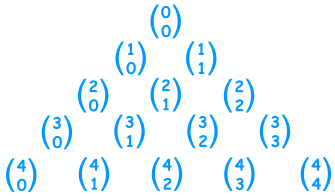
Pascal üçgeninde her satırdaki sayıların toplamı (n 0'dan başlamak üzere 2^n).
Bunu ispatlamak çok kolay→ ilk sayı 1 ve her yeni satıra atlayışımızda bulunduğumuz satırdaki sayıları 2 kere toplama işleminde kullanıyoruz.
kombinasyon toplam formülüne göre C(n-1, k-1) + C(n-1, k) = C(n, k)
Vee işte sana ispat. ↓

Ekleme: kombinasyon toplam formülünü de sorabilirsin diye açıklıyorum:
C(n,k) n elemanlı kümenin k elemanlı kümelerini oluşturma yollarının sayısıdır.
Biz bu kümeden bir x elemanını göz önünde bulunduralım. Geriye n-1 eleman kalır.
Biz bu x elemanını k kümesine aldık diyelim. Geriye seçeceğimiz (k-1) kadar eleman var. Onun değeri de C(n-1, k-1)'dir.
Eğer ki bu x elemanını k kümesine almazsak, seçeceğimiz k kadar eleman var (sonuçta k sayıda eleman seçiyoruz). Öyleyse onu da C(n-1, k) şeklinde hesaplarız.
Bu iki koşuldaki seçim sayısının toplamı, aslında hiçbir şeyi değiştirmediğimiz için C(n,k)'ya eşit olacaktır.
C(n-1, k-1) + C(n-1, k) = C(n, k)
Ekleme 2:
İlk soruda üstte bahsettiğim kombinasyon toplam formülünü kullanırsak C(n+1, n-2)=56 elde ederiz
(n+1)*n*(n-1)/3!=56 buradan n=7 çıkar.
2. soru ispata göre 2^10 olur.
Zaten son soru da C(19,0)+C(19,1)+C(19,2)+...+C(19,19) toplamının yarısına eşittir. 2^18
_____

Pascal üçgeninde her satırdaki sayıların toplamı (n 0'dan başlamak üzere 2^n).
Bunu ispatlamak çok kolay→ ilk sayı 1 ve her yeni satıra atlayışımızda bulunduğumuz satırdaki sayıları 2 kere toplama işleminde kullanıyoruz.
kombinasyon toplam formülüne göre C(n-1, k-1) + C(n-1, k) = C(n, k)
Vee işte sana ispat. ↓
Ekleme: kombinasyon toplam formülünü de sorabilirsin diye açıklıyorum:
C(n,k) n elemanlı kümenin k elemanlı kümelerini oluşturma yollarının sayısıdır.
Biz bu kümeden bir x elemanını göz önünde bulunduralım. Geriye n-1 eleman kalır.
Biz bu x elemanını k kümesine aldık diyelim. Geriye seçeceğimiz (k-1) kadar eleman var. Onun değeri de C(n-1, k-1)'dir.
Eğer ki bu x elemanını k kümesine almazsak, seçeceğimiz k kadar eleman var (sonuçta k sayıda eleman seçiyoruz). Öyleyse onu da C(n-1, k) şeklinde hesaplarız.
Bu iki koşuldaki seçim sayısının toplamı, aslında hiçbir şeyi değiştirmediğimiz için C(n,k)'ya eşit olacaktır.
C(n-1, k-1) + C(n-1, k) = C(n, k)
Ekleme 2:
İlk soruda üstte bahsettiğim kombinasyon toplam formülünü kullanırsak C(n+1, n-2)=56 elde ederiz
(n+1)*n*(n-1)/3!=56 buradan n=7 çıkar.
2. soru ispata göre 2^10 olur.
Zaten son soru da C(19,0)+C(19,1)+C(19,2)+...+C(19,19) toplamının yarısına eşittir. 2^18
İspat sorman güzel bir şey, birçok kişi bu kombinasyon formüllerini ezberleyip geçerler.
_____

Pascal üçgeninde her satırdaki sayıların toplamı (n 0'dan başlamak üzere 2^n).
Bunu ispatlamak çok kolay→ ilk sayı 1 ve her yeni satıra atlayışımızda bulunduğumuz satırdaki sayıları 2 kere toplama işleminde kullanıyoruz.
kombinasyon toplam formülüne göre C(n-1, k-1) + C(n-1, k) = C(n, k)
Vee işte sana ispat. ↓

Ekleme: kombinasyon toplam formülünü de sorabilirsin diye açıklıyorum:
C(n,k) n elemanlı kümenin k elemanlı kümelerini oluşturma yollarının sayısıdır.
Biz bu kümeden bir x elemanını göz önünde bulunduralım. Geriye n-1 eleman kalır.
Biz bu x elemanını k kümesine aldık diyelim. Geriye seçeceğimiz (k-1) kadar eleman var. Onun değeri de C(n-1, k-1)'dir.
Eğer ki bu x elemanını k kümesine almazsak, seçeceğimiz k kadar eleman var (sonuçta k sayıda eleman seçiyoruz). Öyleyse onu da C(n-1, k) şeklinde hesaplarız.
Bu iki koşuldaki seçim sayısının toplamı, aslında hiçbir şeyi değiştirmediğimiz için C(n,k)'ya eşit olacaktır.
C(n-1, k-1) + C(n-1, k) = C(n, k)
Ekleme 2:
İlk soruda üstte bahsettiğim kombinasyon toplam formülünü kullanırsak C(n+1, n-2)=56 elde ederiz
(n+1)*n*(n-1)/3!=56 buradan n=7 çıkar.
2. soru ispata göre 2^10 olur.
Zaten son soru da C(19,0)+C(19,1)+C(19,2)+...+C(19,19) toplamının yarısına eşittir. 2^18
_____

Pascal üçgeninde her satırdaki sayıların toplamı (n 0'dan başlamak üzere 2^n).
Bunu ispatlamak çok kolay→ ilk sayı 1 ve her yeni satıra atlayışımızda bulunduğumuz satırdaki sayıları 2 kere toplama işleminde kullanıyoruz.
kombinasyon toplam formülüne göre C(n-1, k-1) + C(n-1, k) = C(n, k)
Vee işte sana ispat. ↓

Ekleme: kombinasyon toplam formülünü de sorabilirsin diye açıklıyorum:
C(n,k) n elemanlı kümenin k elemanlı kümelerini oluşturma yollarının sayısıdır.
Biz bu kümeden bir x elemanını göz önünde bulunduralım. Geriye n-1 eleman kalır.
Biz bu x elemanını k kümesine aldık diyelim. Geriye seçeceğimiz (k-1) kadar eleman var. Onun değeri de C(n-1, k-1)'dir.
Eğer ki bu x elemanını k kümesine almazsak, seçeceğimiz k kadar eleman var (sonuçta k sayıda eleman seçiyoruz). Öyleyse onu da C(n-1, k) şeklinde hesaplarız.
Bu iki koşuldaki seçim sayısının toplamı, aslında hiçbir şeyi değiştirmediğimiz için C(n,k)'ya eşit olacaktır.
C(n-1, k-1) + C(n-1, k) = C(n, k)
Ekleme 2:
İlk soruda üstte bahsettiğim kombinasyon toplam formülünü kullanırsak C(n+1, n-2)=56 elde ederiz
(n+1)*n*(n-1)/3!=56 buradan n=7 çıkar.
2. soru ispata göre 2^10 olur.
Zaten son soru da C(19,0)+C(19,1)+C(19,2)+...+C(19,19) toplamının yarısına eşittir. 2^18
Uzun uzun yazdığın, yada en azından koyduğun için çok teşekkür ederim. Pascal üçgeninin ispatını anladım. Ama C(n-1, k-1) + C(n-1, k) = C(n, k) şunu tam olarak anlayamadım. c(5,3) diyelim. C(n-1, k-1) içinden bir tane seçtiğimizde, geriye kalanları kaç farklı şekilde seçebileceğimizi verir. Yani c(4,2). Şimdi bu sayı ile ilkini seçme olasılığımızı çarparsak (n/k ile çarparsak yani) c(n,k) ya ulaşmış oluruz. Toplama nereden geldi anlamadım.
1.) Bir tanesini seçtiğimizde C(n-1, k-1) geriye kalanları nasıl bulacağımızı verir. Ama o başta seçtiğimiz (sabitlediğimiz, k kümesinde aldığımız değil) elemanı k kümesine koyup koymayacağımız belli değil, biz C(n-1, k-1)'i hesaplayarak o başta sabitlediğimiz elemanı k kümesine koyduğumuzda oluşan durumları hesaplıyoruz.
2.) 1'de bahsettiğim gibi, o seçtiğimiz (seçtiğimiz demeyelim de sabitlediğimiz diyelim, kafa karıştırıcı olmasın) elemanı k kümesine koyma zorunluluğumuz yok.
____
Her neyse farklı kelimlerle anlatmaya çalışayım.
Şimdi C(5,3), 5 elemanlı kümeden 3 elemanlı kümeleri oluşturabilme sayısını verir.
Biz buradan bir elemanı sabitleyelim. (Tekrar söylüyorum bu elemanı oluşturduğumuz 3 elemanlı kümeye koyma zorunluluğumuz yok.)
Şimdi bu sabitlediğimiz elemanı 3 elemanlı kümelere koyduğumuz ve koymadığımız durumları hesaplayıp toplarsak, temel olarak seçim işleminde hiçbir şeyi değiştirmediğimiz için C(5,3)'na ulaşacağız.
Bu sabitlediğimiz elemanı önce yok sayalım. (4 eleman kaldı)
Diyelim bu elemanı kümeye almaya karar verdik (geriye seçilecek 2 eleman kaldı, onu hesaplamak istersek → C(4,2))
Kümeye almazsak (geriye seçilecek 3 eleman kaldı, onu da C(4,3) şeklinde hesaplarız.)
Bunları toplarsak 5 elemanlı kümeden oluşturulabilecek 3 elemanlı kümelerin sayısını bulmuş oluruz.
C(4,2)+C(4,3)= C(5,3)
İspat aslında çok temiz, bunu anlarsan kombinasyonun özünü anlamış olursun. Bakış açını genişletir.
Ama yine de cebirsel ispat istiyorsan o da aşağıda:

Yazdıklarınla ilgili
1.) Bir tanesini seçtiğimizde C(n-1, k-1) geriye kalanları nasıl bulacağımızı verir. Ama o başta seçtiğimiz (sabitlediğimiz, k kümesinde aldığımız değil) elemanı k kümesine koyup koymayacağımız belli değil, biz C(n-1, k-1)'i hesaplayarak o başta sabitlediğimiz elemanı k kümesine koyduğumuzda oluşan durumları hesaplıyoruz.
2.) 1'de bahsettiğim gibi, o seçtiğimiz (seçtiğimiz demeyelim de sabitlediğimiz diyelim, kafa karıştırıcı olmasın) elemanı k kümesine koyma zorunluluğumuz yok.
____
Her neyse farklı kelimlerle anlatmaya çalışayım.
Şimdi C(5,3), 5 elemanlı kümeden 3 elemanlı kümeleri oluşturabilme sayısını verir.
Biz buradan bir elemanı sabitleyelim. (Tekrar söylüyorum bu elemanı oluşturduğumuz 3 elemanlı kümeye koyma zorunluluğumuz yok.)
Şimdi bu sabitlediğimiz elemanı 3 elemanlı kümelere koyduğumuz ve koymadığımız durumları hesaplayıp toplarsak, temel olarak seçim işleminde hiçbir şeyi değiştirmediğimiz için C(5,3)'na ulaşacağız.
Bu sabitlediğimiz elemanı önce yok sayalım. (4 eleman kaldı)
Diyelim bu elemanı kümeye almaya karar verdik (geriye seçilecek 2 eleman kaldı, onu hesaplamak istersek → C(4,2))
Kümeye almazsak (geriye seçilecek 3 eleman kaldı, onu da C(4,3) şeklinde hesaplarız.)
Bunları toplarsak 5 elemanlı kümeden oluşturulabilecek 3 elemanlı kümelerin sayısını bulmuş oluruz.
C(4,2)+C(4,3)= C(5,3)
İspat aslında çok temiz, bunu anlarsan kombinasyonun özünü anlamış olursun. Bakış açını genişletir.
Ama yine de cebirsel ispat istiyorsan o da aşağıda:

1.) Bir tanesini seçtiğimizde C(n-1, k-1) geriye kalanları nasıl bulacağımızı verir. Ama o başta seçtiğimiz (sabitlediğimiz, k kümesinde aldığımız değil) elemanı k kümesine koyup koymayacağımız belli değil, biz C(n-1, k-1)'i hesaplayarak o başta sabitlediğimiz elemanı k kümesine koyduğumuzda oluşan durumları hesaplıyoruz.
2.) 1'de bahsettiğim gibi, o seçtiğimiz (seçtiğimiz demeyelim de sabitlediğimiz diyelim, kafa karıştırıcı olmasın) elemanı k kümesine koyma zorunluluğumuz yok.
____
Her neyse farklı kelimlerle anlatmaya çalışayım.
Şimdi C(5,3), 5 elemanlı kümeden 3 elemanlı kümeleri oluşturabilme sayısını verir.
Biz buradan bir elemanı sabitleyelim. (Tekrar söylüyorum bu elemanı oluşturduğumuz 3 elemanlı kümeye koyma zorunluluğumuz yok.)
Şimdi bu sabitlediğimiz elemanı 3 elemanlı kümelere koyduğumuz ve koymadığımız durumları hesaplayıp toplarsak, temel olarak seçim işleminde hiçbir şeyi değiştirmediğimiz için C(5,3)'na ulaşacağız.
Bu sabitlediğimiz elemanı önce yok sayalım. (4 eleman kaldı)
Diyelim bu elemanı kümeye almaya karar verdik (geriye seçilecek 2 eleman kaldı, onu hesaplamak istersek → C(4,2))
Kümeye almazsak (geriye seçilecek 3 eleman kaldı, onu da C(4,3) şeklinde hesaplarız.)
Bunları toplarsak 5 elemanlı kümeden oluşturulabilecek 3 elemanlı kümelerin sayısını bulmuş oluruz.
C(4,2)+C(4,3)= C(5,3)
İspat aslında çok temiz, bunu anlarsan kombinasyonun özünü anlamış olursun. Bakış açını genişletir.
Ama yine de cebirsel ispat istiyorsan o da aşağıda:

Şimdi C(5,3), 5 elemanlı kümeden 3 elemanlı kümeleri oluşturabilme sayısını verir.
Biz buradan bir elemanı sabitleyelim. (Tekrar söylüyorum bu elemanı oluşturduğumuz 3 elemanlı kümeye koyma zorunluluğumuz yok.)
Şimdi bu sabitlediğimiz elemanı 3 elemanlı kümelere koyduğumuz ve koymadığımız durumları hesaplayıp toplarsak, temel olarak seçim işleminde hiçbir şeyi değiştirmediğimiz için C(5,3)'na ulaşacağız.
Bu sabitlediğimiz elemanı önce yok sayalım. (4 eleman kaldı)
Diyelim bu elemanı kümeye almaya karar verdik (geriye seçilecek 2 eleman kaldı, onu hesaplamak istersek → C(4,2))
Kümeye almazsak (geriye seçilecek 3 eleman kaldı, onu da C(4,3) şeklinde hesaplarız.)
Bunları toplarsak 5 elemanlı kümeden oluşturulabilecek 3 elemanlı kümelerin sayısını bulmuş oluruz.
C(4,2)+C(4,3)= C(5,3)

bu sabitledimiz elemanı yok saydık 4 eleman kaldı yani c(5,3) idi , c(4,3) oldu ,
diyelim bu elemanı kümeye almaya karar verdik geriye seçilecek 2 eleman kaldı diyorsunuz bunu nerden anladınız? kümeye almazsak geriye 3 eleman kaldı diyorsunuz bunu nerden anladınız? k diye bir küme yok söylediniz acıklamada c(n,k) ifadesinde k dediğimiz k elemanlı alt kümelerin eleman sayısını belirtiyor k kümesi ne oluyor?bu olayları kümeleri vererek acıklarsanız daha anlasılır olur
yardımcı olursanız sevinirim.
uğraş sonucu anladım yukarda anlatılıyor eğer anlamayan olursa özel mesaj atsın anlatirim
