1.Bir çocuk 10 basamaklı bir merdiveni her adımda 1 ya da 2 basamak çıkarak kaç değişik şekilde çıkabilir?
2.Bir bakterinin çoğalması incelenmektedir. Her bakteri saatte bir kez bölünüp yeni bir bakteri oluşturmaktadır. Her yeni bakteri de 1 saatte olgunlaştıktan sonra (ilk saat bölünmüyor) ilk bakteri gibi bölünmeye başlamaktadır. Başlangıçta 1 olgun bakteri ile işe başlanırsa 10 saat sonunda mikroskobumuzda kaç bakteri gözlemleriz?
Not:Bölünme sonrası oluşan 2 bakteriden sadece birisi olgunlaşmak için 1 saat bekleyecektir diğeri normal bölünmesine devam edecektir.
3.Sadece 1 ve 0 lardan oluşan ve 2 tane 0 ın yan yana gelmediği kaç tane 10 basamaklı sayı yazılabilir?
Ör: 1101011110 , 1111111111
Dikkat: 0101110101 sayısı 10 değil 9 basamaklıdır
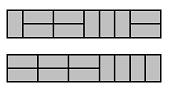
4.2x10 büyüklüğünde bir tahta 2x1 büyüklüğündeki dominolarla, dominoları kesmemek ve üst üste getirmemek şartıyla, kaç değişik şekilde kaplanabilir?
Ör:
5.Herbirinin içine 1 tane balon bağlanmış 10 tane kutu yan yana dizilmiştir. Her balonun ipi en fazla bir yanındaki kutuya yetişmektedir. Balonlar her kutuda 1 balon olmak şartıyla bu 10 kutuya yerleştirilip kutuların kapakları kapatılacaktır. Bu işlem kaç değişik şekilde yapılabilir?