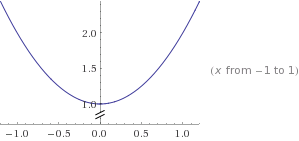
Koordinat sistemi üzerinde bir y=x² fonksiyonunun grafiğini çizelim.
Çizersek , çizdiğimiz grafiğin tepe noktasınının Orjin üzerinde (0,0) noktasında yer aldığını farkederiz.
->Tepe Noktası Kaydırılınca Ne olur?
Misal , yukarıdaki parabol.Görüldüğü üzere , tepe noktası y=1 ordinatı üzerinden yayılmaktadır.
İşte bu yüzden , hemen y=a.x²+1 yazabiliriz , çünkü bilindiği üzere +1 değeri fonksiyonun sabit terimidir ve sabit terim parabol'ün y ekseninini kestiği nokta idi.
Parabol'ün Tepe Noktası T(r,k) olmak üzere , y=ax²+c parabol'ü için. T(1,2)'i örnek gösterelim.Burada , x=0 için , y=c olduğu ayan beyan ortada yani verilen parabol'ün tepe noktasının ordinatı 2'dir.
O halde , bu parabol , orjinden 2 birim yukarı taşınmıştır.
Peki Parabol , sağa veya sola kaydırılırsa ne olur?
Şimdi yine y=ax² parabolünü ele alalım.Bu parabol x eksenini (2,0) noktasında kessin.
E biliyoruz ki , x eksenini kesen nokta fonksiyonun , y=0 için denkleminin kökleridir.
Peki , size bir soru , Parabol 2.dereceden fonk.grafiği değil mi ? O halde en basit kökü 2 olan parabol'ü yazalım.
y=(x-2)² dersiniz hemen elbet.
Peki , bu parabol y'yi (0,4)'te değilde 3 de de kesebilir.Peki bu nasıl mümkün olabilir?
Ancak , bir başkatsayının varlığıyla ! Çünkü , başkatsayıya göre parabol'ün kollarının açıklığı değiştikçe başkatsayıda değişecektir.
O halde , başkatsayı dediğim y=ax² parabol'ündeki a=> başkatsayıdır.