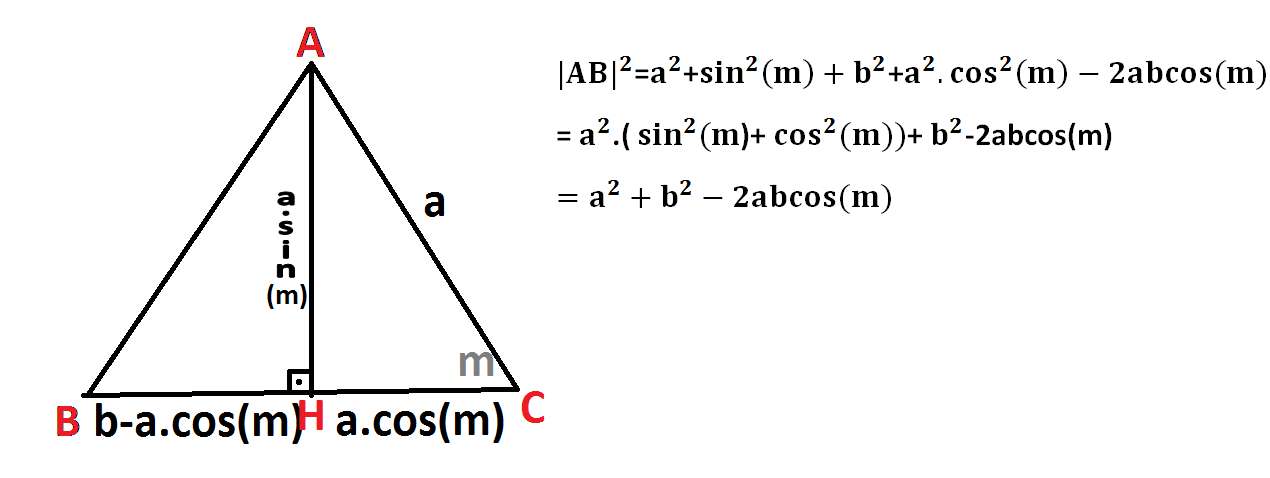İspat 1 :
İspat 2 :
Aslında, kosinüs teoremini ispatlarken kullandığımız sin²(m)+cos²(m)=1 özelliği de buradan ispatlanabilir. Soldaki üçgende değil de sağdaki üçgende pisagor yaparsak şöyle olur:
a²sin²(m)+a²cos²(m)=a²
Her tarafı a'ya bölersek;
sin²(m)+cos²(m)=1 olur.
İspat 3 :
Buradan sinüslü alan formülü de ispatlanabilir. Dikkat ederseniz, yükseklik a.sin(m), taban da b . Dolayısıyla alan da a.b.sin(m).1/2 olur.
İspat 4 :
Buradan biraz zor olsa da sinüs teoremi de ispatlanabilir. Açıların hepsini yazarız. Daha sonra A köşesindeki iki açının toplamının kosinüsünü toplam formülüyle buluruz. Daha sonra AB kenarının kosinüs teoremindeki eşitini yazarız. Dikkat ederseniz sinüs teoremindeki bilinmeyen sayımız 4'e düşüyor: sin(m), cos(m), a ve b. Hatta sin(m) yerine √1-cos²(m) yazarsak 3'e düşer. Daha sonra sinüs teoremi bu üç bilinmeyenle yazılır. Ve sonuçta, bu üç bilinmeyenin her değeri için sinüs teoreminin sağlandığı görülür. İspat biter.