1. f(x) doğrusal bir fonksiyon olsun f(1) = 2 ve f(2) = 3 ise f⁻¹(4)ün değerini bulunuz.
Çözüm:
f(x) doğrusul bir fonksiyon ise,
f(x) = ax+b dir.
f(1) = a+b = 2
f(2) = 2a+b= 3
-2/a+b =2
2a +b = 3
-2a -2b = -4
2a + b = 3
+__________
-b = -1, b = 1
b = 1 ise a+b = 2 yerine yazalım;
a+1 = 2
a = 1
O hâlde, f(x) = 1.x + 1 = x +1 dir.
f⁻¹(x) = x-1
f⁻¹(4) = 4 - 1 = 3 olarak bulunur.
2. R → R ye tanımlı bire bir ve örten f ve g fonksiyonları için f⁻¹(2) = 3 ve g (4) = 2 ise (f⁻¹og)⁻¹(3) değerini bulunuz.
Çözüm:
Not : (fog)⁻¹= g⁻¹of⁻¹ dir. O hâlde,
f⁻¹(2) = 3 ⇒ f(3) = 2 dir.
(f⁻¹og)⁻¹(3) = (g⁻¹of)(3) = g⁻¹{f(3)}
= g⁻¹(2) = 4
3. f(x) =2x-13x-4fonksiyonun tanım ve değer kümelerini bulunuz.
Çözüm:
3x- 4 = 0
3x = 4
x = 4/3
Tanım kümesi R - {43}
f⁻¹(x) =4x-13x-2
3x+ 2= 0
x = 2/3
Değer kümesi IR - {23}
4.: Aşağıdaki fonksiyonların tanım kümelerini bulunuz.
a) f(x) = ³√x+1
b) f(x) = √x²-1
Çözüm:
a) n = 3 tek olduğundan tanım kümesi x+1 ile aynı, R dir.
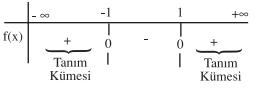
b) x² - 1 ≥ 0
(x - 1)(x + 1) = 0
x = -1, x = 1
Tanım kümesi = (-∞, -1] ∪ [ 1, +∞)
5. f(x) = √log1/10(2x-1)fonksiyonunun en geniş tanım kümesini bulunuz.
Çözüm:
2x -1 > 0 ve log1/10(2x-1) ≥ 0 için tanımlı
2x > 1 ve log1/10(2x-1) ≥ 0
x > 1/2 ve - log (2x - 1) ≥ 0 (Eşitsizliği - ile çarpmak ya da bölmek eşitsizliğin yönünü değiştirir)
log (2x - 1) ≤ 0
2x - 1 ≤ 1
x ≤ 1
O hâlde tanım kümesi (1/2 , 1] olur.