1
f(x) fonksiyonunun A(2,3) noktasındaki teğetinin eğimi -2 ve g(x) fonksiyonunun apsisi x=3 olan noktasındaki teğetinin eğimi 4'tür. Buna göre h(x)=(gof)(x) eğrisinin, apsisi x=2 olan noktasındaki teğetinin eğimini bulalım.
Öncelikle eğrinin eğimini bulmak için türevini alalım,
h'(x)=g'(f(x)).f'(x), bize x=2'deki eğimi soruluyor:
h'(2)=g'(f(2)).f'(2),
yukarıda
f(x)'in apsisi 2 olan noktadaki eğimi yani f'(2)=-2,
g(x)'in apsisi 3 olan noktadaki eğimi yani g'(3)=4 verilmiş. Bunlar da bize lazım olan değerler olup:
h'(2)=g'(3).f'(2)=4.(-2)=(-8) elde ederiz.
2
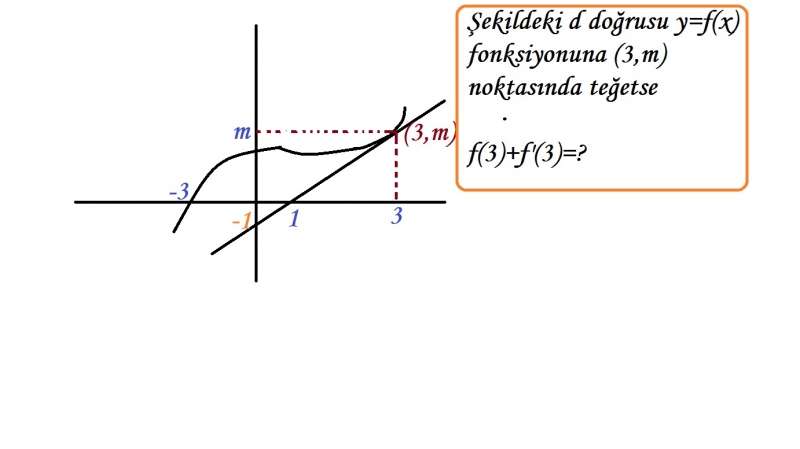
f(3)=m olduğu görülüyor.
f'(3) için "fonksiyonun x=3 noktasındaki teğetinin eğimini" bulalım.
Benzerlikten faydalanırsak [m/(3-1)]=[(1/1)], m=2
f(3)=2
f'(3)=2/2=1
2+1=3
3
y=(mx+4)/(nx+p) eğrisinin simetri merkezinin koordinatı (-2,3) ise m ve p pozitif tam sayılarının çarpımı en az kaç olur?
Simetri merkezinin koordinatında apsis bize düşey asimptotu (aynı zamanda paydanın kökü=tanımsızlayan değer) verir,
nx+p=0
x=(-p/n)=-2, p/n=2 olur.
Ordinat ise yatay asimptotu verir ki bunu da ifadenin limitinden bulabiliriz, m/n'dir.
m/n=3
p/n=2,
m/p=3/2, m.n=> en az 6 olur.
4
Bir hareketlinin t saniyede aldığı yol metre olarak
s(t)=2t²-8t+17 ise bu hareketlinin 10. saniyedeki hızını bulalım.
İfadenin 1. türevi bize hızı, 2. türevi ise ivmeyi verir.
1. türev: 4t-8
sorulan: 10. saniyedeki hız: 4.10-8=32