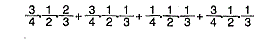[korkmazserkan]

1) ÖSS sınavını Neslihan Arda ve sezen isimli 3 öğrencinin kazanma olasılıkları sırasıyla tür
ÖSS sınavını en az ikisinin kazanma olasılığı kaçtır?

çözüm1)
ÖSS sınavını en az 2 kişi kazanacaksa

          neslihan   arda   sezen

          kazanır   kazanır  kaybeder



          kazanır   kaybeder kazanır



          kaybeder kazanır   kazanır



          kazanır    kazanır   kazanır

gibi dört durum vardır

olasılığıda

= tür



2) Üstlerinde 1,1,3,4,4,5 yazılı altı kart bir torbaya konuluyor. Torbadan rasgele toplamı, sırayla ve çekilenler geri konmaksızın üç kart çekilip, üstlerindeki rakamlardan çekiliş sırasına göre oluşturulan üç basamaklı sayının 3’e bölünme olasılığı nedir?

çözüm 2)
113---3 tane
114---6 tane
115---3 tane
344----3 tane
445---3 tane
1.3.4.5 de 24 tane
toplam 42 tane olur
3 ile bölen 18 tanedir
olsalık bulunur


3) 600 sayısının pozitif tamsayı bölenlerinden seçilen bir sayının
3 ün katı olma olasılığı kaçtır?

çözüm 3)
600 ün bölenlerine bakalım
3.2³.5²
pozitif bölen sayısı 2.4.3=24
3 ün katı olmayan bölenler 4 ve 2 dir
4.2=8
3ün katı olanlar 24-8=16


4) Hilesiz bir zar ve madeni para ile bir oyun oynanıyor. Oyunun kuralına göre önce zar atılıyor ve ardından zarın üst yüzeyine gelen sayı kadar madeni para art arda havaya atılıyor.
Buna göre, zar bir kez atıldığından paraların art arda 4 kez tura gelme olasılığı kaçtır ?

çözüm 4)
4 gelen zarda 4 tane tura gelmesi

5 gelen zarda 5 tane tura gelmesi

6 gelen zarda 4 tane tura gelmesi




5) Bir deneye ait E örnek uzayı, E={A,B,C} dir A,B,B ayrık olaylar ve
2.PA)=3.P(B)=6.P(C) olduğuna göre P(A∪B) kaçtır?

çözüm 5)
E={A,B,C} ise
P(A)+P(B)+p(C)=1 dir
2P(A)=3P(B)=6P(C)=6k olsun
P(A)=3k
P(B)=2k
P(C)=k olur
3k+2k+k=1
k=
A∩B=boş küme olduğundan
P(A∪B)=P(A)+P(B)
P(A∪B)=3k+2k=5k=5.1/6=5/6