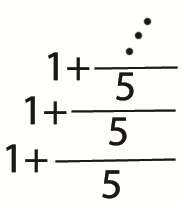
Öncelikle kusura bakmayın, resimle soru eklemenin yasak olduğunu biliyorum ama ifadenin anlaşılır olabilmesi için ilk soruyu resimle soruyorum. Bu editörde paya merdiven eklemeyi beceremedim.
İşleminin sonucu kaçtır? (5/4)
2) m ve n gerçel sayılardır.
-4<m<=3
-6<=n<-3
olduğuna göre m²+n² nin alabileceği en küçük tam sayı deeğeri?
Bu soruda anlamadığım bir nokta var. ilk ifadenin karesini aldığı zaman 3 olan yere 0 gelmiş ve ifade şöyle olmuş;
0<=m²<16
Buradan sonra kafam karıştı. Yardımlarınız için teşekkürler...