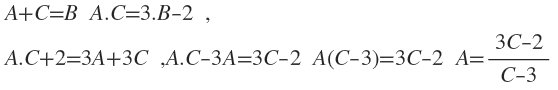1-
A+C=B
A.C=3.B-2 ise A ' nın C cinsinden eşiti nedir?
2-
41a ve 1b6 üç basamaklı sayılardır.
(41a).(1b6) çarpımı 9 ile tam bölünebild. göre a+b toplamının alabilecegi en büyük değer kaçtır?
3-
p ve q birbirlerinden farklı asal sayılar olmak üzere,
a= p².q
b= q³
c= a².b⁴ ise c sayısını tam bölebilen p ve q dışında kaç pozitif tam sayı vardır?
4- x+y < z+t
y+t < x+z
x+t = y+z koşullarına uyan x y z ve t gerçek sayıları için
I. x>y
II. z>y
III. z>t yargılarından hangileri kesin doğrudur?
5- a-4 < b-2 < a+5 old. göre,
a²+b²-2ab ifadesinin alabileceği kaç farklı tamsayı değeri vardır?