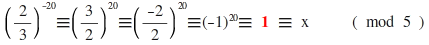Hocam,
Aşağıdaki sorunun çözümünü rica ediyorum. Teşekkürler.
=(2/3)^-20≡x (Mod.5) ise x=?
Aşağıdaki sorunun çözümünü rica ediyorum. Teşekkürler.
=(2/3)^-20≡x (Mod.5) ise x=?
Ben çözümünü yazabilirim.
Modüler aritmetik sorularında karşımıza kesirli ifadeler çıktığında; payda bulunan sayının yerine o sayının verilen moda göre denkliklerini yazarak kesri tam sayı yapmaya çalışırız. Burada da 2/3 kesri verilmiş. Paydaki sayıya bakalım: 2. Şimdi verilen modda yani mod 5'de 2'nin denklik sınıflarından bazılarını yazalım.
2≡7≡12 (mod 5) olduğundan 2/3 kesrinde (mod 5'de) 2 yerine 7 veya 12 yazılabilir. Ancak 7 bir işimize yaramaz. Çünkü 7/3 de tam sayı değil. O zaman bir de 12'yi deneyelim. 12/3 sayısı 4'e eşit olduğundan bir tam sayıdır. O halde şöyle bir denklik yazılabilir:
2/3≡4 (mod 5)
Şimdi de soruda bizden istenene bakalım.
(2/3)-20≡x verilmiş ve x sorulmuş.
2/3≡4 (mod 5) bulduğumuzdan dolayı soruda 2/3 gördüğümüz yere 4 yazabiliriz. Öyleyse soru şöyle olacaktır:
"4-20≡x (mod 5)
Şimdi bunu da şöyle düzenleyebiliriz:
(4-1)20≡x (mod 5)
4-1=1/4'tür zaten. Onun yerine 1/4 yazabiliriz. Soru şöyle olur:
(1/4)20≡x (mod 5)
Şimdi başta anlattığım metottan gidip 1/4'ün mod 5'deki denkliğini bulalım.
1≡6≡11≡16(mod 5) olduğu için kesirde 1 gördüğümüz yere 16 yazabiliriz. Yazarsak zaten kesrimiz 4'e eşit olur. O halde soru şöyle olur:
420≡x (mod 5)
Şimdi de 4 yerine onun mod 5'deki denklerinden biri olan -1'i yazalım.
(-1)20≡x(mod 5)
(-1)20 sayısı da zaten 1'e eşittir. (-1'in çift kuvvetleri 1 yapar.)
O halde x=1'dir.
Modüler aritmetik sorularında karşımıza kesirli ifadeler çıktığında; payda bulunan sayının yerine o sayının verilen moda göre denkliklerini yazarak kesri tam sayı yapmaya çalışırız. Burada da 2/3 kesri verilmiş. Paydaki sayıya bakalım: 2. Şimdi verilen modda yani mod 5'de 2'nin denklik sınıflarından bazılarını yazalım.
2≡7≡12 (mod 5) olduğundan 2/3 kesrinde (mod 5'de) 2 yerine 7 veya 12 yazılabilir. Ancak 7 bir işimize yaramaz. Çünkü 7/3 de tam sayı değil. O zaman bir de 12'yi deneyelim. 12/3 sayısı 4'e eşit olduğundan bir tam sayıdır. O halde şöyle bir denklik yazılabilir:
2/3≡4 (mod 5)
Şimdi de soruda bizden istenene bakalım.
(2/3)-20≡x verilmiş ve x sorulmuş.
2/3≡4 (mod 5) bulduğumuzdan dolayı soruda 2/3 gördüğümüz yere 4 yazabiliriz. Öyleyse soru şöyle olacaktır:
"4-20≡x (mod 5)
Şimdi bunu da şöyle düzenleyebiliriz:
(4-1)20≡x (mod 5)
4-1=1/4'tür zaten. Onun yerine 1/4 yazabiliriz. Soru şöyle olur:
(1/4)20≡x (mod 5)
Şimdi başta anlattığım metottan gidip 1/4'ün mod 5'deki denkliğini bulalım.
1≡6≡11≡16(mod 5) olduğu için kesirde 1 gördüğümüz yere 16 yazabiliriz. Yazarsak zaten kesrimiz 4'e eşit olur. O halde soru şöyle olur:
420≡x (mod 5)
Şimdi de 4 yerine onun mod 5'deki denklerinden biri olan -1'i yazalım.
(-1)20≡x(mod 5)
(-1)20 sayısı da zaten 1'e eşittir. (-1'in çift kuvvetleri 1 yapar.)
O halde x=1'dir.
C-1
Kesirin derecesinde bulunan negatifliği yok etmek için kesri ters çeviririz.
(2/3)-20=(3/2)20
Rasyonel ifadelerde pay kısmına bölüm tam sayı olana kadar mod'u ekliyoruz.
(3+5)/2=4
3/2=4 (mod 5)
Yani (2/3)-20 = 420 = x (mod 5)
41=4 (mod 5)
42=1 (mod 5)
Derece tek ise sonuç kalan 4, çift ise kalan 1 oluyormuş.
420 = 1 (mod 5)
(2/3)-20=1 (mod 5)
Kesirin derecesinde bulunan negatifliği yok etmek için kesri ters çeviririz.
(2/3)-20=(3/2)20
Rasyonel ifadelerde pay kısmına bölüm tam sayı olana kadar mod'u ekliyoruz.
(3+5)/2=4
3/2=4 (mod 5)
Yani (2/3)-20 = 420 = x (mod 5)
41=4 (mod 5)
42=1 (mod 5)
Derece tek ise sonuç kalan 4, çift ise kalan 1 oluyormuş.
420 = 1 (mod 5)
(2/3)-20=1 (mod 5)
Eline sağlık Mat. Çözümünü görmemiştim 
Sağol, önemli değil. 
Elinize sağlık, teşekkür ederim çözümler için.
Kutlarım.Güzel, açıklamalı çözümler.
Çözümü kısaltalım.

Çözümü kısaltalım.