özel tanımlı fonksiyonlar-çarpan

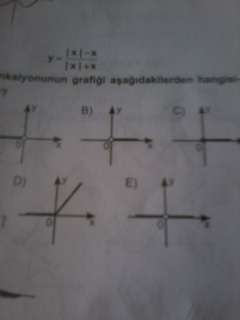
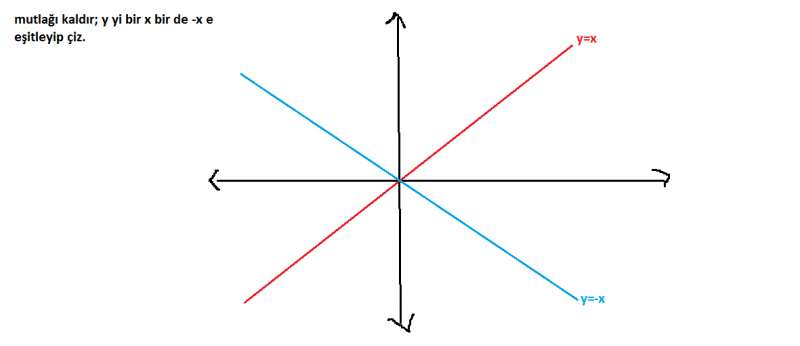
3) |y|=|x| denkleminin grafiğini çiziniz.

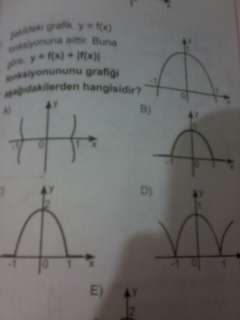
4) f(x)=f(|x|) fonksiyonunun grafiğini çiziniz.

5) 73.145 işleminde her çarpan 1 artırlırsa işlemin sonucu kaçtır?(219)

3. sorunun cevabı :

5) Kaç artar demek istediniz galiba.
73=x, 145=y ise yeni çarpım (x+1)(y+1)=xy+x+y+1 olacak yani çarpım x+y+1=219 artmış olacak.

1) Bu tip mutlak değerli sorularda fonksiyonu parçalı hale getirerek yorumlamak her zaman işimizi kolaylaştıracaktır. Bu nedenle x in sıfırdan büyük ve sıfırdan küçük olduğu değerlerdeki fonksiyonlara bakabiliriz.

x'in sıfırdan büyük değerleri için x mutlak değerden x olarak çıkacağından fonksiyonumuz;
f(x)=(x-x)/(x+x)=0 fonksiyonu olacaktır.

x'in sıfırdan küçük değerleri için x mutlak değerden -x olarak çıkacağından fonksiyonumuz;
f(x)=(-2x)/0 olacağından tanımsız olacaktır bu durumda x<0 için fonksiyonumuz tanımsızdır. aynı şekilde paydayı sıfır yapan tüm değerler için fonksiyonumuz tanımsız olacağından; x≤0 için fonksiyonumuz tanımsızdır.Fonksiyon (0,+∞) aralığında tanımlıdır. Bu durumda grafiğimiz yalnızca x>0 için çizilecektir.Yani grafiğimiz f(x)=0 için;



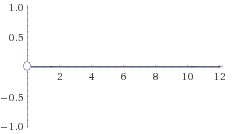
(Sıfır fonksiyonu tanımsız yaptığından açık aralık aldık)

evet eksik yazmışım artar olacaktı teşekkür ederim

2)1. yol ;
İlk olarak fonksiyonun denklemini yazalım;
Fonksiyon x eksenini 1 ve -1 noktalarında kestiğinden;

f(x)=a(x-1)(x+1) ve y eksenini 1 noktasında kestiğinden;

1=-a dan a=-1 olacaktır yani f(x)=-(x-1)(x+1) olacaktır.

Bu durumda |f(x)|=|-(x-1)(x+1)| olacaktır.

|f(x)| i parçalı biçimde ifade edersek;

x>1 için; (x-1)(x+1)

-1<x<1 için; -(x-1)(x+1)

x<-1 için; (x-1)(x+1)

olacaktır.

f(x)+|f(x)| için her durumu f(x) le toplarsak;

x>1 için; 0

-1<x<1 için; -2x²+2

x<-1 için; 0

fonksiyonları elde edilir. Her bir aralığa uygun grafikler çizilirse;



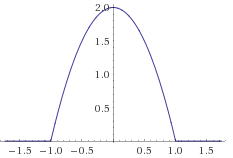
grafiği elde edilir.

2) 2. yol;
y=|f(x)| in grafiği, aşağıdaki adımlar sırayla izlenerek daha kısa biçimde çizilebilir

--y=f(x) in grafiği çizilir.
--x ekseninin altındaki kısmın x eksenine göre simetriği grafiğe eklenir.
--x ekseninin altındaki kısım silinir.
--Elde edilen grafik y=|f(x)| in grafiği olur.

Sonra grafik üzerinde toplama yaparsak;



grafiğini elde ederiz.

4)f(x)=f(|x|) fonksiyonunun grafiğini çiziniz.

f(x)=f(|x|) olabilmesi için;

Fonksiyon ya sabit olmalı, yada çift fonksiyon olmalıdır. Bu durumda f(x) fonksiyonu ya;

y=n şeklinde olmalı yada y=x^2m+n , y=cosx ... biçiminde olmalıdır.

Bu durumda örnek grafikler verecek olursak;

f(x)=n e örnek olarak;



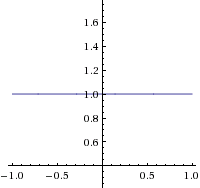
Çift fonksiyona örnek olarak;