Dershane öğretmenim bir soru sordu.
Soru şu:
z=1+cos220+i.sin220
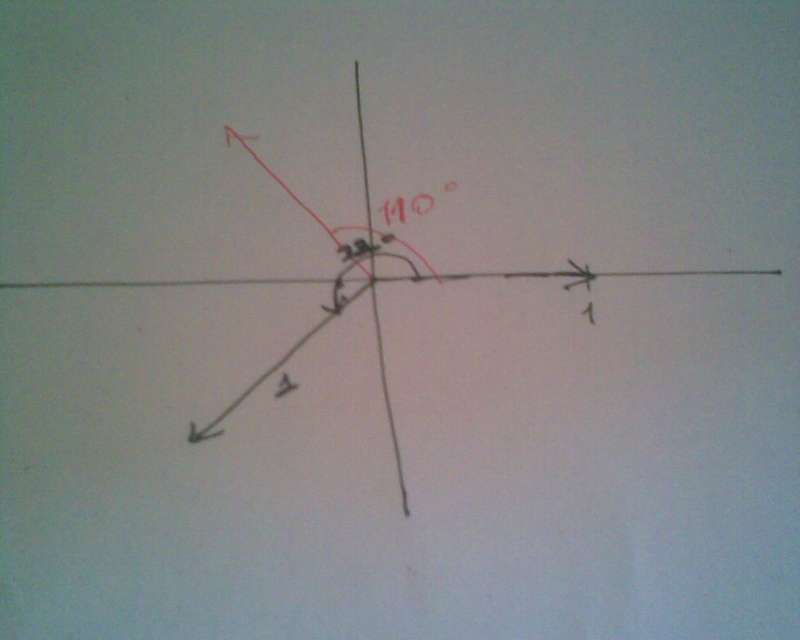
karmaşık sayısının esas argümenti kaç derecedir ?
Bende şöyle çözüm yaptım.
1+2cos²110-1+i.2.sin110.cos110=
2cos²110+i.2.sin110.cos110=2cos110(cis110+isin110)=
-2cos70(-cos70+isin70)=
2cos70(cos70-isin70)=
2cos70(cos(-70)+isin(-70))=
2cos70(cos290+isin290)
|z|=2cos70
Arg(z)=290
Ancak öğretmenim çözümümün yanlış olduğunu cevabın 110 olduğunu söyledi.
Çözümümden eminim ama aklıma takıldı.