.Aklıma takılan bir nokta.

Dershane öğretmenim bir soru sordu.
Soru şu:
z=1+cos220+i.sin220
karmaşık sayısının esas argümenti kaç derecedir ?
Bende şöyle çözüm yaptım.
1+2cos²110-1+i.2.sin110.cos110=
2cos²110+i.2.sin110.cos110=2cos110(cis110+isin110)=
-2cos70(-cos70+isin70)=
2cos70(cos70-isin70)=
2cos70(cos(-70)+isin(-70))=
2cos70(cos290+isin290)
|z|=2cos70
Arg(z)=290

Ancak öğretmenim çözümümün yanlış olduğunu cevabın 110 olduğunu söyledi.
Çözümümden eminim ama aklıma takıldı.

1+2cos²110-1+i.2.sin110.cos110
2cos²110+i.2.sin110.cos110
=2cos110(cis110+isin110)
=2cos110.cis110

|z|=2cos110
Arg(z)=110

çözüm burada bitmiş zaten.

Benzerlerine buradan (Karmaşık Sayılar-Argüment İşlemleri Güzel Sorular ve Çözümleri) ulaşabilirsiniz.

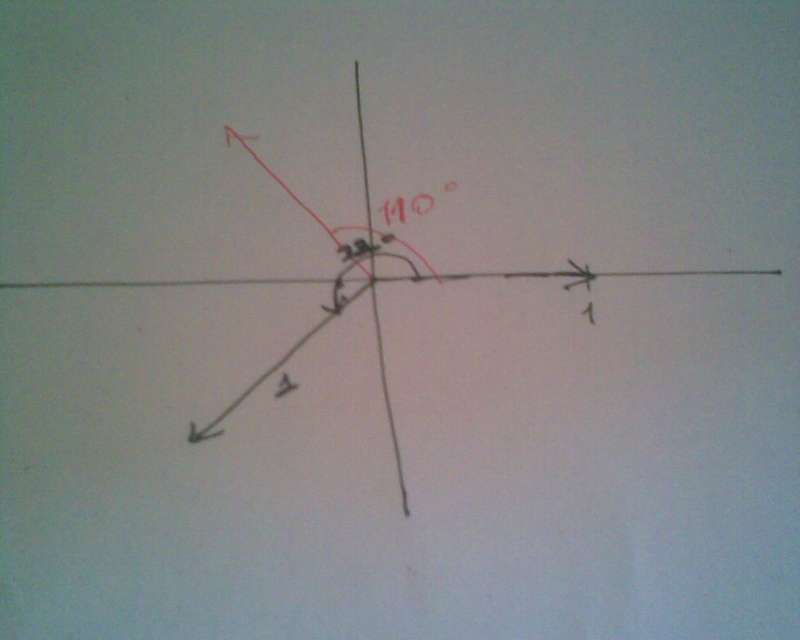
bize hocamız böyle öğretti bu kadar işleme gerek yok

Vektör yolunu biliyorum maatematik.
z=1+cos220+i.sin220
1=z1=cis0
cos220+i.sin220=z2=cis220 olmak üzere;

Bu durumda Arg(z1+z2)=-70=290 olmalı. Sen toplam vektörünü yukarı da yapmışsın. Ama z1 ve z2 parelelkenar oluşturmalı.

|z|=2cos110=> cosinüs ikinci bölgede eksi olduğundan |z|'de negatif olamayacağından işleme devam etmeliyiz. İşlemi burada kesemeyiz. |z|'in pozitif olması içinde bölge değiştirmeliyiz.

melek çözümün doğru... öğretmenin gözden kaçırmış olmalı r>0 haklısın

Mantıklı