2.SORU:
3.SORU:
MatematikciFM 21:56 15 Oca 2011 #2
Mert46; 2. soru 20, 3. soru 80, 1. soru 200/3 mü?
1.soru 180 2.soru 20 3.soru 80
MatematikciFM 22:07 15 Oca 2011 #4
2 ve 3 ü doğru çözmüşüm ama çözüm bayağı uzun. Dİğer arkadaşlar kısa bir çözüm bulurlar belki. Olmazsa sonra yazarım.
1. soruda verilenlerle bulunması zor gözüküyor.
1. soruda verilenlerle bulunması zor gözüküyor.
çözümlerinizi bekliyorum. teşekkürler
gereksizyorumcu 01:57 16 Oca 2011 #6
1.
EKC ve EBC üçgenlerine bakalım bu iki üçgenin tabanları aynı yğksekliklri oranıysa 1/2 dir dolayısıyla da alanları oranı 1/2 olmalıdır
ELC üçgeninin alanı S olsun öyleyse
2.(4+s)=9+s olmalıdır → s=1 bulunur
buradan |LC|/|LK|=1/4 bulunur ve A(BLK)=36 bulunur paralelkenarın 1/4 ünün alanı=36+9=45 olduğuna göre tüm alan =180 bulunur
2.
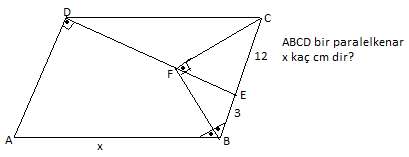
F noktsından CB ye paralel çizelim
açıları yazdığımızda bu paralelin diküçgenin kenarortayı olduğu da görülüyor yani uzunluğu 15/2 olmalı
ayırdığı parçalarsa 15/2 ve 9/2 olur
paralllikte oluşan benzerliği yazarsak
(9/2)/12=(15/2)/x → x=20 bulunur
3.
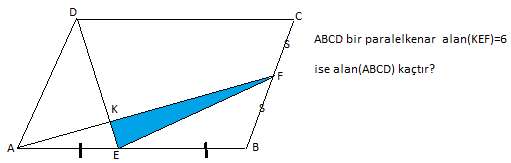
A(AKE)=s olsun
A(ADE)=12+2s olacağından A(ADK)=12+s olur
aynı şekilde DF yi birleştiip A(ADF)=24+4s olacağından da A(DKF)=12+3s olur
bu bulunan 4 alan |DK| ve |KE| üzerinde oluştuğundan oranları eşit olmalıdır
(12+3s)/6=(12+s)/s
→ s²+2s-24=0 → s=4 veya s=-6 , alan olduğundan s=-6 almayız, s=4 ise
A(AEF)=10 olur tüm alan da bu üçgenin 8 katı olacağından 80 bulunur.
EKC ve EBC üçgenlerine bakalım bu iki üçgenin tabanları aynı yğksekliklri oranıysa 1/2 dir dolayısıyla da alanları oranı 1/2 olmalıdır
ELC üçgeninin alanı S olsun öyleyse
2.(4+s)=9+s olmalıdır → s=1 bulunur
buradan |LC|/|LK|=1/4 bulunur ve A(BLK)=36 bulunur paralelkenarın 1/4 ünün alanı=36+9=45 olduğuna göre tüm alan =180 bulunur
2.
F noktsından CB ye paralel çizelim
açıları yazdığımızda bu paralelin diküçgenin kenarortayı olduğu da görülüyor yani uzunluğu 15/2 olmalı
ayırdığı parçalarsa 15/2 ve 9/2 olur
paralllikte oluşan benzerliği yazarsak
(9/2)/12=(15/2)/x → x=20 bulunur
3.
A(AKE)=s olsun
A(ADE)=12+2s olacağından A(ADK)=12+s olur
aynı şekilde DF yi birleştiip A(ADF)=24+4s olacağından da A(DKF)=12+3s olur
bu bulunan 4 alan |DK| ve |KE| üzerinde oluştuğundan oranları eşit olmalıdır
(12+3s)/6=(12+s)/s
→ s²+2s-24=0 → s=4 veya s=-6 , alan olduğundan s=-6 almayız, s=4 ise
A(AEF)=10 olur tüm alan da bu üçgenin 8 katı olacağından 80 bulunur.
gereksizyorumcu 02:17 16 Oca 2011 #7
3. soru için ikinci ve daha kısa bir yol daha gördüm
FE yi uzatıp AD yi kestirelim kesim noktası Z olsun. |AD|=2.|AZ| ve |ZE|=|EF| olur.
FAZ üçgeninde DE kesen olacak şekilde menelaus uygulayalım.
(|AD|/|AZ|).(|ZE|/|EF|).(|FK|/|KA|)=1
(2/3).(1/1).(|FK|/|KA|)=1 → (|FK|/|KA|)=3/2 → A(AKE)=(2/3).6=4 bulunur.
burdan sonra da zaten A(ABCD)=8.10=80 olur.
FE yi uzatıp AD yi kestirelim kesim noktası Z olsun. |AD|=2.|AZ| ve |ZE|=|EF| olur.
FAZ üçgeninde DE kesen olacak şekilde menelaus uygulayalım.
(|AD|/|AZ|).(|ZE|/|EF|).(|FK|/|KA|)=1
(2/3).(1/1).(|FK|/|KA|)=1 → (|FK|/|KA|)=3/2 → A(AKE)=(2/3).6=4 bulunur.
burdan sonra da zaten A(ABCD)=8.10=80 olur.
MatematikciFM 02:17 16 Oca 2011 #8
Üstadım, 1. soruyu ben görememiştim iyi görmüşsünüz. 3. sorudaki çözümünüz de benimki kadar uzun. Ben de az sonra kendi çözümümü yazayım. Ama şu 2. sorudaki anlatımınızı anlamadım. F den çektiğiniz paralel nasıl kenarortay oldu?
MatematikciFM 02:23 16 Oca 2011 #9
Üstadım, bende özel teorem antipatisi var. Tek çözüm, o olmadıkça başvurmuyorum. Bazen ştandart olmak iyi oluyor.
MatematikciFM 02:47 16 Oca 2011 #10 
Diğer çözümlü sorular alttadır.
.10. sınıf Çözümlü Dörtgen Soruları .10. sınıf Çözümlü Paralelkenar Soruları Çözümlü Geometri Soruları Dörtgenlerde Alanla İlgili Çözümlü Sorular Dörtgenlerde Benzerlik Çözümlü Sorular Paralelkenarla İlgili Çözümlü Sorular
Tüm Etiketler
Tüm Etiketler