Polinomlar

1-3.dereceden bir P(x) polinomunun, (x-3)(x-2)(x+1)çarpımı ile bölümünden kalan x²−3x+1 'dir. P(3-x) polinomunun x+1 ile bölümünden kalan 45 ise, P(x)'in baş katsayısı?

2-p(x)=p(x+1)+2x³-x+1 eşitliğini sağlayan p(x) polinomunun x ile bölümünden kalan 3'tür.p(x) polinomunun x-2 ile bölümünden kalan kaçtır?

3-p(x³+2)=3x'üzeri6+4x³+5 ise, p(x²) polinomunun x-√3 ile bölümünden kalan=?

4-p(x)=x³+ax²+2x+1 polinomunun x-1 ile bölümünden elde edilen bölüm polinomunun katsayıları toplamı 2 ise a =?

5-p(x) başkatsayısı 2 olan, dördüncü dereceden ve x³-x²+7 ile kalansız bölünüyor.bu polinomun x+1 ile bölümünden kalan 15 ise p(x)'in katsayıları toplamı=?

Cevaplarsanız çok sevinirim.şimdiden teşekkürler ve bir de çok güzel ve yararlı bir forum olmuş admine teşekkürler.

C-1

Bölme işlemine göre aşağıdaki gibi yazabiliriz:
P(x)=(x-3)(x-2)(x+1)Q(x)+x²-3x+1
P(x) 3. dereceden imiş, 1. dereceden 3 ifadenin çarpımı 3. dereceden olacağından Q(x) 0. dereceden yani sabit olmalıdır.
P(3-x)'te x+1 ile kalanı bulmak için x=-1 yazarız, demek ki P(3-(-1))=P(4)=45 imiş.
P(4)=1.2.5.Q(4)+16-12+1=10Q(4)+5=45
Q(4)=4=Q(x) (Sabit polinom olduğundan)
P(x)=(x-3)(x-2)(x+1).4+x²-3x+1
Başkatsayı x³'lü terimin katsayısı olacağından, 4 olur.
İyi günler.

C-2

P(x) polinomunun x ile bölümünden kalanı bulmak için x=0 alırız. P(0)=3 olur.
P(x) polinomunun x-2 ile kalanını bulmak için x=2 alırız, yani P(2) sorulmuş.
x=0'ı yazarsak; P(0)=P(1)+1 olur.
P(1)=2 çıkar.
x=1'i yazarsak; P(1)=P(2)+2-1+1=P(2)+2 olur. P(1)=2 olduğundan P(2)=0 çıkar.
İyi günler.

C.5


P(x) = (x³-x²+7).(2x+n)+0
P(-1)=15

P(-1)=5.(-2+n)=15
-2+n=3 , n=5 bulunur.

P(1) = (1-1+7).(7) = 49 bulunur.

C-3

P(x³+2)=3x⁶+4x³+5=3(x³)²+4x³+5=3(x³+2-2)²+4(x³+2-2)+5
x³+2 yerine x koyalım:
P(x)=3(x-2)²+4(x-2)+5 olur. x yerine x² koyarsak;
P(x²)=3(x²-2)²+4(x²-2)+5
x-√3 ile kalanı bulmak için x=√3 alırız;
3(3-2)²+4(3-2)+5=3+4+5=12 olur.
İyi günler.

C-4

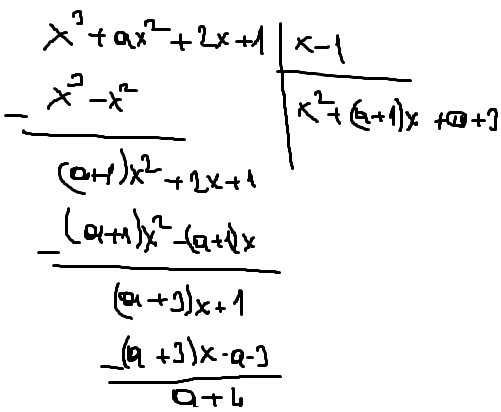
Katsayılar toplamı 1+a+1+a+3=2a+5 olur. 2a+5=2 ise a=-3/2 olur.
İyi günler.

C.4

Bi farklı çözümde ben koyayım.Horner metoduylada buradan çözüme ulaşılabiliyor.
Horner yöntemiyle üst tarafa bölünenin katsayılarını yazın.Daha sonra sol tarafa x=1 yazın.
Daha sonra horner yöntemiyle çözerseniz bölüme 1 , a+1 , a+3 geliyor kalanada a+4 geliyor.

1+a+1+a+3 = 2a+5 = 2 , 2a=-3 , a=-3/2 bulunur.

eğer horner yöntemi bilmiyorsanız söyleyin resimlede ekliyelim.

bu kadar çabuk cevap vereceğinizi düşünmemiştim.çok teşekkürler

Aslında (ufak bi hata) burada Q(x)'yerine farklı bi ifade yazmak daha yerinde olur çünkü polinom 3.dereceden eğer xli bi ifade yazılırsa 4.dereceden gibi anlaşılmalara çekebiliyor kendini buraya a şeklinde farklı şeyler yazarsanız daha doğru olur.(Hocalar sınavlarda bunlardan kırıyor.kendiimden biliyorum sırf bu hatadan dolayı quizde 2-3 puan kırdı.)

Çözümde Q(x)'in sabit polinom olması gerektiğini belirttim, sabit polinom olması gerektiğini söyleyince puan kırılmaması gerekir gibi geliyor. Sonuçta orada Q(x) yazmak illa ki 1 ve üstü derecelerden bir ifade olmasını gerektirmiyor. Uyardığın için teşekkür ederim.
İyi günler.