Eşitsizlik

1. 2x-1>√(2x²-3x+1) eşitsizliğinin ÇKsı? = [1,+∞)

2. x²/ ( √(x+3)+√(4-x) )>0 sağlayan tamsayılar kaç tane? =7

3.
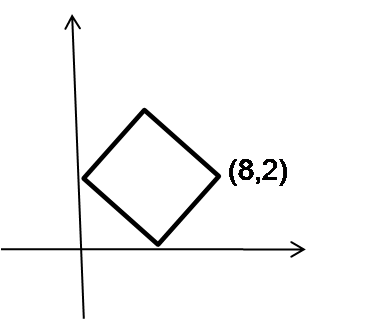
Karenin alanı? =40

1. 2x-1>√(2x²-3x+1) eşitsizliğinin ÇKsı? = [1,+∞)

Her iki tarafın karesini alalım.

4x²-4x+1>2x²-3x+1
2x²-x>0
2x²>x olur.
2x>1
x=[1,+∞)

Soru 2:
Payda sıfır olamaz, ayrıca çift dereceli kökün içi negatif olamaz, o halde;
x+3>0 x>-3 ve 4-x>0 4>x x<4 oluyor.
Dolayısıyla -3≤x≤4 oldu. Bu aralıkta sekiz tane sayı var.
Fakat biz o ifadenin sıfırdan büyük olmasını istiyoruz, dolayısıyla x 0 olamaz. Aralığımız
[-3, 4]-{0} oldu. Bu aralıkta 7 tane tamsayı vardır.
İyi günler.

teşekkürler

eşitsizlikte sadeleştirme nasıl yapıyosun?

Sadeleştirme yapmamış.
Karesini almış.Çünkü karesini aldığında eşitsizlik yön değiştirmeyecektir.

3. sorunun resmini çekip eklemen daha sağlıklı olacaktır.

Sadeleştirme yapmadım karesini aldım.
2x²>x olur.
2x>1

2x.x>x
2x>1 bunda anlaşılmayacak ne var ?

Ben bu noktaya dikkat etmemişim. x<0 ise eşitsizlik yön değiştiririr.
O yüzden şu şekilde daha garanti olacaktır.
2x²>x
2x²-x>0
x.(2x-1)>0
x=0 x=1/2
++++++(0)------------(1/2)+++++
+++ kısımlar bizim çözüm kümemizin elemanı.
Ancak kareköklü ifadenin içi 0dan küçük olamayacağından soldaki kısımı alamayız.Çünkü kareköklü ifadenin içini 0dan küçük yapar. Bunu
deneyerek görebiliriz.
Bu durumda Ç.K=(1/2,sonsuz)
Kareköklü ifadenin içindeki denklemin kökleri 1/2 ve 1 dir.
1/2 ve 1i deneyelim. (1/2 zaten dahil değil denememizi gerek yok.)
1 eşitliği sağlar bu durumda
Ç.K=[1,sonsuz)

1. 2x-1>√(2x²-3x+1) eşitsizliğinin ÇKsı? = [1,+∞)

Her iki tarafın karesini alalım.

4x²-4x+1>2x²-3x+1
2x²-x>0
2x²>x olur.
2x>1

Aslında aynı şey Kısa kestim karekökün içerisi tabii kide negatif olamaz. Bir nevi şu oluyor ;

4x²-4x+1>2x²-3x+1
2x²-x>0
2x²>x olur.
2x>1
x>1/2 ise ; 1/2den büyük bir değer olacak!Bunedenle ilk değer 1 oluyor ondan kısa kestim anlaşılır diye.

1/2 den büyük değeri 0,6 neden almıyoruz?