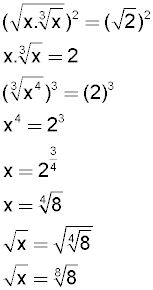1) √(x∛x)=√2 olduğuna göre, √x nedir? (cevap=8√8)
2)A={1,2,3,4,5,6} kümesinin 4lü permütasyonlarının kaç tanesinde 1 veya 2 bulunur? (cevap=336)
3) Analitik düzlemde, (x,y)=(3,a)+k₁(-3,-6)
(x,y)=(2,2)+k₂(-4,b) doğrularının ortak noktası olmadığına göre a+b toplamı hangisi olamaz? (cevap=-4)
4)Analitik düzlemde, A(k,k+1) B(2k,1-k) noktaları veriliyor. AB vektörünün x ekseni üzerinde izdüşüm vek. uzunluğu 12 birim ise k'nın negatif değeri kaçtır? (cevap=-12)
10.Sınıfa gitmiyorum ama umarım iyi anlatabilirim
2)A={1,2,3,4,5,6} kümesinin 4lü permütasyonlarının kaç tanesinde 1 veya 2 bulunur? (cevap=336)
İlk olarak 4lü permütasyonlarının sayısını bulalım daha sonra ise 1 ve 2 nin bulunduğu permütasyonları çıkartalım.
P(6,4)=6!/2!=6.5.4.3=360 olur.
4lü permütasyonları ; _ _ 1 2 olsun.Bu durumda 1 ve 2 dışındaki rakamların 2 yere yerleştirmemiz gerekecek.
P(4,2)=4!/2!=4.3=12 oldu fakat yukarı da _ _ 1 2 olacağı gibi 1 2 _ _ 'de olabilir o halde ; 12.2 = 24 farklı dizilim yapılabilir.
360-24=336 olacaktır.
Eğer şey de kafan karışırsa 1 2 _ _ yaptın _ _ 1 2 yaptın e neden 2 1 _ _ ve _ _ 2 _1 neden olmadı dersen önemli olan 1 ve 2 olmuyor o iki kutucuğa gelecek sayılar oluyor sağdaki 2 kutucuğa 12 sayı soldakine 12 sayı olunca 24 değişik olur
ikinize de teşekkürler..
svsmumcu bu konu artık 11. sınıf konusu, yani sende 11'de görcen
diğer analitik geometri sorularına da bakarsanız sevinirim
2. için:
A kümesinin 4lü permütasyonu=P(6,4)
A kümesinin 1 ve 2 hariç diğer elemanlarından oluşan 4lü permütasyonu=P(4,4)
A kümesinin 4lü permütasyonundan A kümesinin 1 ve 2 hariç diğer elemanlarından oluşan 4lü permütasyonunu çıkarırsak sonuca ulaşırız.
P(6,4)-P(4,4)
360-24=336
C.4
AB vektörü=B-A=(k,-2k)
k=12
-k=-12
İnternetim yok
Foruma üye olmana gerek yok! Facebook hesabınla yorumlarını bekliyoruz!
