1.SORU:
f(x)=mx2+2x-3 fonksiyonun en büyük değeri 1 olduğuna göre x ∈[-2,3] için f(x) in alabileceği birbirinden farklı tamsayı değerlerin toplamı kaçtır?
2.SORU:
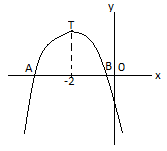
yukardaki şekilde f(x)=-x2-4x+c parabolünün grafiği verilmiştir.|AB|=2 birim olduğuna göre f(x) in en büyük değeri kaçtır?
f(x)=mx2+2x-3 fonksiyonun en büyük değeri 1 olduğuna göre x ∈[-2,3] için f(x) in alabileceği birbirinden farklı tamsayı değerlerin toplamı kaçtır?
2.SORU:

yukardaki şekilde f(x)=-x2-4x+c parabolünün grafiği verilmiştir.|AB|=2 birim olduğuna göre f(x) in en büyük değeri kaçtır?
2) Şekilde (-2.y) noktası tepe noktası olarak verilmiş. Parabol tepe noktasına göre simetrik olduğundan ve |AB|=2 birim olduğundan A(-3.0) ve B(-1,0) noktasıdır. x yerine -1 yazıp sıfıra eşitlersek,
-12-4.(-1)+c=0 c=-3
c yi bulduktan sonra x yerine -2 yazıp tepe noktasının ordinatını bulalım,
-22-4(-2)-3=1
-12-4.(-1)+c=0 c=-3
c yi bulduktan sonra x yerine -2 yazıp tepe noktasının ordinatını bulalım,
-22-4(-2)-3=1
1) Parabolün en büyük değeri 1 ise prabolün tepe noktasının ordinatı 1miş. Tepe noktasının ordinatı veren formül şu şekildeydi,

buradan
[(4m.(-3)-4]/4m=1
-12m-4=4m, m=-1/4
parabolümüz şu şekli aldı, -x2/4+2x-3=0

buradan
[(4m.(-3)-4]/4m=1
-12m-4=4m, m=-1/4
parabolümüz şu şekli aldı, -x2/4+2x-3=0
1. soruda tam sayı değerlerin toplamı sorulmuş
Alp hocamızın bulduğu -x²/4+2x-3 parabolünden ve bu parabolün [-2,3] aralığında artan olmasından hareketle
f(-2)=-8
f(3)=3/4=0,75
olduğuna göre sürekliliğin sonucu olarak bu parabol bu aralıkta -8 ile 0 arasındaki her tamsayı değeri alır bunların toplamıda -8.9/2=-36 bulunur.
Alp hocamızın bulduğu -x²/4+2x-3 parabolünden ve bu parabolün [-2,3] aralığında artan olmasından hareketle
f(-2)=-8
f(3)=3/4=0,75
olduğuna göre sürekliliğin sonucu olarak bu parabol bu aralıkta -8 ile 0 arasındaki her tamsayı değeri alır bunların toplamıda -8.9/2=-36 bulunur.
1. soruda tam sayı değerlerin toplamı sorulmuş
Alp hocamızın bulduğu -x²/4+2x-3 parabolünden ve bu parabolün [-2,3] aralığında artan olmasından hareketle
f(-2)=-8
f(3)=3/4=0,75
olduğuna göre sürekliliğin sonucu olarak bu parabol bu aralıkta -8 ile 0 arasındaki her tamsayı değeri alır bunların toplamıda -8.9/2=-36 bulunur.
Alp hocamızın bulduğu -x²/4+2x-3 parabolünden ve bu parabolün [-2,3] aralığında artan olmasından hareketle
f(-2)=-8
f(3)=3/4=0,75
olduğuna göre sürekliliğin sonucu olarak bu parabol bu aralıkta -8 ile 0 arasındaki her tamsayı değeri alır bunların toplamıda -8.9/2=-36 bulunur.
Diğer çözümlü sorular alttadır.
.10. sınıf Parabol Çözümlü Sorular Çözümlü Parabol Soruları Parabol İle İlgili Çözümlü Sorular Parabol Soruları
Tüm Etiketler
Tüm Etiketler
