gereksizyorumcu 20:02 21 Tem 2012 #11
dedim ya yuvarlak masada masaya ilk oturan için yer seçilmez o tek şekilde masaya oturur ama masayı açar yani dönme simetrisini ortadan kaldırır. (10 kişinin 9! şekilde dizilmesi bu yüzden , kalan 9 kişi için bi kısıtlama, yoksa 9! şekilde dizileceklerdir)
bu soruda da çiftlerden birini seçip tek şekilde oturturuz. sonra karşısında eşi gelecektir. diğer çiftin birini 6 yerden birine karşısına da eşini, kalan 4 yere de 4! şekilde eşsizleri.
ben önce eşsiz olanları yerleştireceğim derseniz
3! şekilde onlar yerleşir (masa sabitlendi)
çiftlerden birini alıp 4 yerden birine eşini de karşısına
diğer çiftten bi kişiyi oluşan 6 yerden birine ve eşini karşısına
3!.4.6
bu soruda da çiftlerden birini seçip tek şekilde oturturuz. sonra karşısında eşi gelecektir. diğer çiftin birini 6 yerden birine karşısına da eşini, kalan 4 yere de 4! şekilde eşsizleri.
ben önce eşsiz olanları yerleştireceğim derseniz
3! şekilde onlar yerleşir (masa sabitlendi)
çiftlerden birini alıp 4 yerden birine eşini de karşısına
diğer çiftten bi kişiyi oluşan 6 yerden birine ve eşini karşısına
3!.4.6
gereksizyorumcu 20:05 21 Tem 2012 #12
bir de not sorun ikiye bölme sorunu değil , öyle olsaydı AaBb için 4 buluyor olurdun. mesela aynı metot 6 kişi (2 tanesi eşsiz) için 8 çıkması gereken cevabı 24 bulur.
gereksizyorumcu 20:07 21 Tem 2012 #13 Hocam yaptığım hatayı anladım,
Bunun gibi iki durumu farklı kabul ediyordum bu yüzden olması gereken sonucun 2 katını buluyordum.
Bulduğum sonucu, yani 288'i ikiye bölmeliydim ve cevap 144 olmalıydı
Bunun gibi iki durumu farklı kabul ediyordum bu yüzden olması gereken sonucun 2 katını buluyordum.
Bulduğum sonucu, yani 288'i ikiye bölmeliydim ve cevap 144 olmalıydı
bunlar yuvarlak masada farklıdır zaten
bir de not sorun ikiye bölme sorunu değil , öyle olsaydı AaBb için 4 buluyor olurdun. mesela aynı metot 6 kişi (2 tanesi eşsiz) için 8 çıkması gereken cevabı 24 bulur.
gereksizyorumcu 20:15 21 Tem 2012 #16 Sorun hangi işlemde peki
İyice aklım karıştı...
cizmeli kedi 21:28 21 Tem 2012 #17
Sayin gereksiz yorumcu aciklamalariniz icin tesekkurler
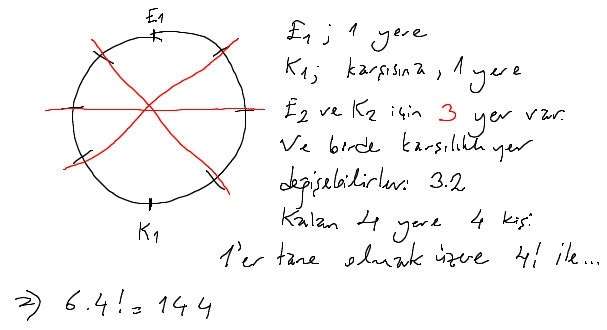
Başka bir soru. Soru benim değil:
8 kişi yuvarlak bir masa etrafına oturacaklardır. Bunlardan belirli üçü yanyana olmak ve belirli ikisi yanyana olmamak şartuyla kaç farklı biçimde oturulabilir?
gereksizyorumcu 01:16 22 Tem 2012 #19
hocam arkadaşlara yardımı olması açısından yazdığınız soruda ufak bi açıklama gerekiyor. yan yana olmaması istenen kişilerle yan yana olması istenen kişilerin kesişim durumu nedir? toplamda kaç kişiler , 3,4,5?
Bu 3 ile 2 (belli) kişi, 8 kişi içinde farklı kişiler. Yâni, bu tanımlanan iki küme-grup "varlık" olarak kesişimleri yok-boş...