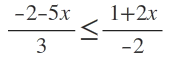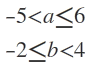[local99]

Yukarıdaki sorularda , mesela aynı yönlü eşitsizlikler taraf tarafa toplanabiliyor .. Bu büyük eşit ya da küçük eşitte'de geçerlimi ?Yukarda taraf tarafa toplanabilir mi ?

Birde eşitsizliğin iki yanı negatif bir sayı ile çarpılınca yön değişiyordu . Yukarıda payda eşitledik paydalar -6 oldu . Paydaları ***ürmek için -6 ile çarpıyoruz ..Sadeleştirmeleri yapıyoruz .. Birbirlerini gtürdükleri için yön değiştirme olayı atlanabilir mi ?

Teşekkürler

[kcancelik]

Evet, taraf tarafa toplama yapabiliriz; ancak eşit işaretini kaldırmamız gerekir. Mesela küçük eşit ile küçük toplarsak küçük eşit yerine küçük koymamız gerekir.
Yön değiştirmeyi yapmalıyız, çünkü bir tarafı - ile çarparken diğerini çarpmıyoruz.
İyi günler.

[local99]

Teşekkürler hocam..

Şunlarada el atarsanız sevinirim


a,b pozitif tam sayı olmak üzere ,

2a+3b >20

old. göre a , en az kaçtır ?

***

x

4

-

2x-1

3

<

1

2

= ?

***

a ve b tam sayıları için ,

-3<x<7
4≤y<8

y-x farkı en çok kaçtır ?

[local99]

a ve b tam sayıları için,

a<b
a.b = 18

old. göre, a kaç farklı değer alabilir ? (cevap 6 diyor :S )

^^Bunun gibi soruları teker teker yazıpta buluyorum sayıları .. Başka bir yolu var mı acaba ?


2-24<x-2<3+2.3

(-4<x<11 diyor ) :s

[svsmumcu26]

a<b
a.b = 18

old. göre, a kaç farklı değer alabilir ?


a b
3 6
2 9
1 18
-6 -3
-9 -2
-18 -1 şeklinde olur.Toplamda 6 tane olur.

a<b olduğundan
a-b< 0 olmalıdır.

[local99]

teşekkürler diğer sorularıda alabilir miyim ?

[svsmumcu26]

a,b pozitif tam sayı olmak üzere ,

2a+3b >20

old. göre a , en az kaçtır ?

2a+3b>20

a=1 için b=7 olursa şart sağlanacaktır açık açık
a=1

[svsmumcu26]

-3<x<7
4≤y<8

y-x farkı en çok kaçtır ?

Sanırım a ve b tamsayıları için değil de x ve y tam sayıları için demek istedin.
Y'yi olabildiğince büyük , x'i olabildiğince küçük seçmeliyiz.


y en çok 7 olabilir.X'de en az -2 olabilir.

7-(-2)=9 olur.(Eğer x ve y tam sayı diyorsa)

[svsmumcu26]

Diğer sorularını da çözebilmem için , daha düzgün yazmalısın Anlaşılmıyor tam.(Tatildeyim , arasıra girebiliyorum.Umarım anlatabilmişimdir.)

[local99]

a,b pozitif tam sayı olmak üzere ,

2a+3b >20

old. göre a , en az kaçtır ?

2a+3b>20

a=1 için b=6 olmalı.Bu durumda 20>20 gibi bir şey olacak buradan sağlamaz.
a=2 için b tam sayı olmaz.
a=3 için , b=5 olursa şart sağlanmış olur.En az a=3 için olur.

hocam bende 3 buldum ama 1 diyor .. :S

Sorular açık gibi hangisini anlayamadınız acaba *düzelteyim hemen