talha.kuru 17:10 29 Ağu 2014 #1
1) Z/7 de, f(3x+4)=2x+5 olduğuna göre, f⁻¹(x) nedir?
cevap: 5x
2) (628+1327+1428+2227)50! sayısının 5 ile bölümünden kalan kaçtır?
cevap: 1
3) (111)¹¹¹+(222)²²²+(333)³³³+...+(999)999 toplamının 6 ile bölümünden kalan kaçtır?
cevap: 11
4)
cevap: 2004
5)
cevap: −3
cevap: 5x
2) (628+1327+1428+2227)50! sayısının 5 ile bölümünden kalan kaçtır?
cevap: 1
3) (111)¹¹¹+(222)²²²+(333)³³³+...+(999)999 toplamının 6 ile bölümünden kalan kaçtır?
cevap: 11
4)
cevap: 2004
5)
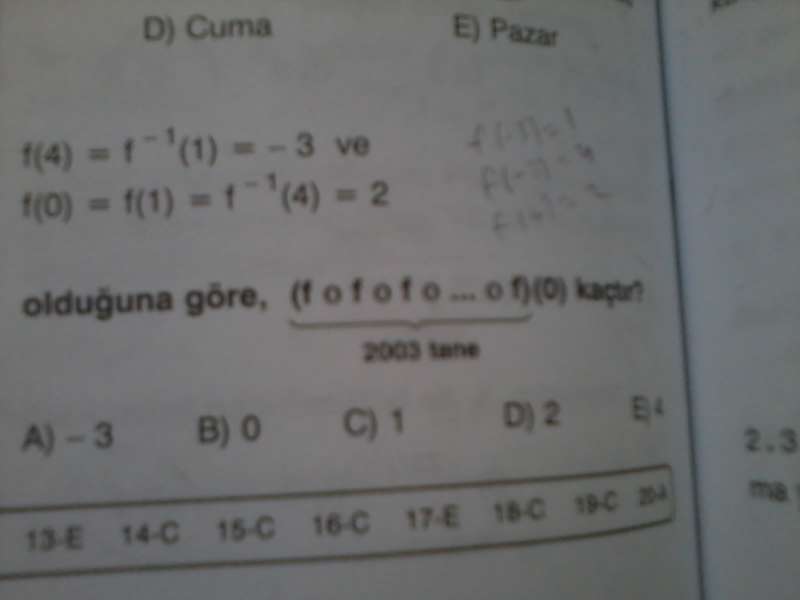
cevap: −3
1. Soru:
f-1(2x+5)=3x+4
burdan f-1(x) sorulduğu için x gördüğüm yere (x-5)/2 yazdım.
f-1(x)=3(x-5)/2 + 4
burda 3/2 ifadesini Z/7'de tam sayı haline getirmek için 3'e 7 ve 7'nin tam katlarını eklemeliyiz. 7 eklediğimizde 10 olur ve 2'ye bölünür, tamsayı çıkar. Bu şekilde 3/2 yerine 5 yazarsak,
5x-25+4 olur o da 5x-21 ifadesine eşittir.
-21 ifadesini de Z/7'ye göre çevirmek için 7'nin tam katı olan 21'i eklersek 0 olur ve geriye 5x kalır.
f-1(2x+5)=3x+4
burdan f-1(x) sorulduğu için x gördüğüm yere (x-5)/2 yazdım.
f-1(x)=3(x-5)/2 + 4
burda 3/2 ifadesini Z/7'de tam sayı haline getirmek için 3'e 7 ve 7'nin tam katlarını eklemeliyiz. 7 eklediğimizde 10 olur ve 2'ye bölünür, tamsayı çıkar. Bu şekilde 3/2 yerine 5 yazarsak,
5x-25+4 olur o da 5x-21 ifadesine eşittir.
-21 ifadesini de Z/7'ye göre çevirmek için 7'nin tam katı olan 21'i eklersek 0 olur ve geriye 5x kalır.
ezio auditore 13:51 01 Eyl 2014 #3
2) (628+1327+1428+2227)50! sayısının 5 ile bölümünden kalan kaçtır?
Çözüm: 628 ≡ 1 (mod5)
1327 ≡ 327 ≡ 2 (mod5)
1428 ≡ 428 ≡ 1 (mod5)
2227 ≡ 227 ≡ 3 (mod5)
Kalanların toplamları: 1+2+1+3 ≡ 2 (mod5)
21 ≡ 2 (mod5)
22 ≡ 4 (mod5)
23 ≡ 3 (mod5)
24 ≡ 1 (mod5)
250! ifadesi 4'ün tam katı olduğundan; cevap "1" olur.
3.) Cevaba "11" demişsin dostum; ama cevap 3 çıkıyor.
Tek sayıların 6'ya bölümlerinden kalan 3, çift sayıların 6'ya bölümlerinden kalan 0 olur.
O halde ifade;
3111.5 olur. (5 tane tek sayı olduğundan.)
31 ≡ 3 (mod6)
32 ≡ 3 (mod6)
..
..
3111 ≡ 3 (mod6)
Son olarak;
3.5=15 ≡ 3 (mod6)
4.) a1 ≡ a
a o a ≡ a2 ≡ ı
a3 ≡ b
a4 ≡ r
a5 ≡ ş
Beş seferde bir tablo devrediyor. Buna göre an ≡ r denkliğinin sağlanabilmesi için n değerinin '5k + 4' ifadesini gerçeklemesi gerekiyor. Bu yüzden cevap 2004 olur.
5.)
İfadeleri teker teker yazarsak;
f(4) = -3
f(-3) = 1
f(0) = 2
f(1) = 2
f(2) = 4
İfade f(0)'dan başlıyor ve bileşke halde devam ediyor.
f(0) = 2
f(2) = 4
f(4) = -3
f(-3) = 1
f(1) = 2
f(0) = 2 ifadesini hariç tutarsak 4 seferden sonra başa dönen bir dizi oluşuyor.
2003-1 = 2002
2002 ≡ 2 (mod4)
Buna göre;
2001. ifade f(2) = 4;
2002. ifade de (yani sonuç) f(4) = -3 olur.
Çözüm: 628 ≡ 1 (mod5)
1327 ≡ 327 ≡ 2 (mod5)
1428 ≡ 428 ≡ 1 (mod5)
2227 ≡ 227 ≡ 3 (mod5)
Kalanların toplamları: 1+2+1+3 ≡ 2 (mod5)
21 ≡ 2 (mod5)
22 ≡ 4 (mod5)
23 ≡ 3 (mod5)
24 ≡ 1 (mod5)
250! ifadesi 4'ün tam katı olduğundan; cevap "1" olur.
3.) Cevaba "11" demişsin dostum; ama cevap 3 çıkıyor.
Tek sayıların 6'ya bölümlerinden kalan 3, çift sayıların 6'ya bölümlerinden kalan 0 olur.
O halde ifade;
3111.5 olur. (5 tane tek sayı olduğundan.)
31 ≡ 3 (mod6)
32 ≡ 3 (mod6)
..
..
3111 ≡ 3 (mod6)
Son olarak;
3.5=15 ≡ 3 (mod6)
4.) a1 ≡ a
a o a ≡ a2 ≡ ı
a3 ≡ b
a4 ≡ r
a5 ≡ ş
Beş seferde bir tablo devrediyor. Buna göre an ≡ r denkliğinin sağlanabilmesi için n değerinin '5k + 4' ifadesini gerçeklemesi gerekiyor. Bu yüzden cevap 2004 olur.
5.)
İfadeleri teker teker yazarsak;
f(4) = -3
f(-3) = 1
f(0) = 2
f(1) = 2
f(2) = 4
İfade f(0)'dan başlıyor ve bileşke halde devam ediyor.
f(0) = 2
f(2) = 4
f(4) = -3
f(-3) = 1
f(1) = 2
f(0) = 2 ifadesini hariç tutarsak 4 seferden sonra başa dönen bir dizi oluşuyor.
2003-1 = 2002
2002 ≡ 2 (mod4)
Buna göre;
2001. ifade f(2) = 4;
2002. ifade de (yani sonuç) f(4) = -3 olur.
talha.kuru 20:02 01 Eyl 2014 #4
3.sorunun cevabı 3 olacak evet,yanlış yazmışım,diğer sorular için de çok teşekkür ederim 