1)'' √674 sayısını en yakın onda birliğe göre tahmin ediniz? ''
674, 25'in karesi olan 625 ile 26'nın karesi olan 676 arasındadır. 625 ile 676 arasını 676-625=51 parçaya bölelim. 674, 676-2/51'e yakın olacaktır. 2/51, 1/10'dan küçük olacağından √674≈25,9 olacaktır.
İyi günler.
İyi günler.
gereksizyorumcu 21:34 18 Eki 2012 #3
26,9 değil de 25,9 yazılacakken son anda ufak bir yazım yanlışı olmuş galiba.
benim takıldığım ise 25,9 mu demeliyiz yoksa 26,0 mı? çünkü sayı 26,0 a daha yakın
benim takıldığım ise 25,9 mu demeliyiz yoksa 26,0 mı? çünkü sayı 26,0 a daha yakın
Düzeltmeniz için teşekkür ederim @gereksizyorumcu. İtirazınızda haklısınız, ben 8. sınıftayken daha çok 1 ondalık basamağa kadar sayıyı buluyorduk, ben ona göre yaptım.
İyi günler.
İyi günler.
Bulduklarınız için çok teşekkür ederim öncelikle . Birde √516 sayısını bulabilirmisiniz?
Bir yöntem daha gördüm internette oda şöyle belki biliyorsunuzdur ben birde o gördüğüm yönteme göre çözdüm doğrumu yanlışmı bilmiyorum ama.
===
Bir yöntem daha gördüm internette oda şöyle belki biliyorsunuzdur ben birde o gördüğüm yönteme göre çözdüm doğrumu yanlışmı bilmiyorum ama.
===
gereksizyorumcu 00:15 19 Eki 2012 #6
forumda bir sayının karekökünü nasıl yakın bi şekilde hesaplayabiliriz aratırsanız iligli konuları bulabilirsiniz.
ben genel olarak karekökü -1/2<b<1/2 olmak üzere a+b şeklinde düşünüp a²+2ab+b²=k ifadesinde b² nin ihmal edilebilecek kadar küçük olduğunu varsayıp k=a²+2ab de k ya en yakın tamkareyi bulup (sizin sorunuz için 676)
b=(k-a²)/2a şeklinde b yi hesaplıyorum
b=(674-676)/52=-1/26 , yani 674 ün kökü 26-(1/26) ya oldukça yakın bi değermiş. bu da onda birlik hassasiyette 26,0 olarak gösterilir.
bu adımlar tekrarlanarak hassasiyeti de arttırabiliriz.
ben genel olarak karekökü -1/2<b<1/2 olmak üzere a+b şeklinde düşünüp a²+2ab+b²=k ifadesinde b² nin ihmal edilebilecek kadar küçük olduğunu varsayıp k=a²+2ab de k ya en yakın tamkareyi bulup (sizin sorunuz için 676)
b=(k-a²)/2a şeklinde b yi hesaplıyorum
b=(674-676)/52=-1/26 , yani 674 ün kökü 26-(1/26) ya oldukça yakın bi değermiş. bu da onda birlik hassasiyette 26,0 olarak gösterilir.
bu adımlar tekrarlanarak hassasiyeti de arttırabiliriz.
gereksizyorumcu 00:17 19 Eki 2012 #7
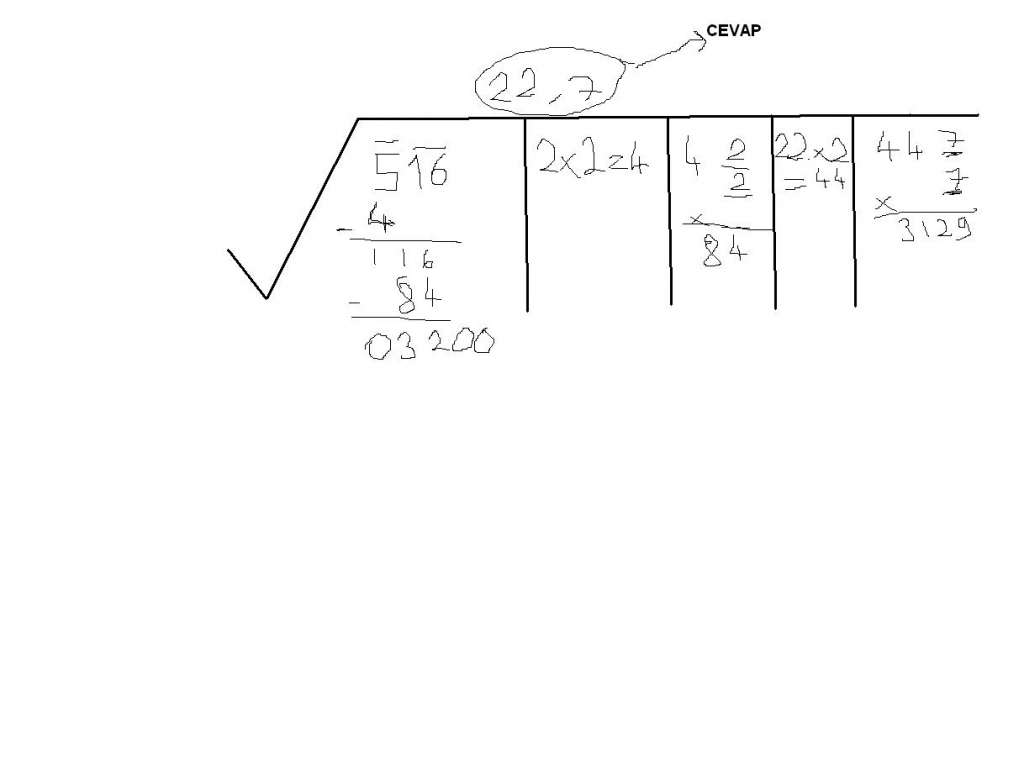
516 örneğini vermişsiniz
516 ya en yakın kare 529=23²
öyleyse bu sayının kökünün 23+((516-529)/46)=23-(13/46)~22,717 ye oldukça yakın olduğunu söyleyebiliriz
516 ya en yakın kare 529=23²
öyleyse bu sayının kökünün 23+((516-529)/46)=23-(13/46)~22,717 ye oldukça yakın olduğunu söyleyebiliriz
tamam 
çok teşekkürler çok yararlı oldu.
çok teşekkürler çok yararlı oldu.
2) √1539 kökünü bulunuz ?
Böyle yüksek sayıların köklerini bulmak için öğretmen ekok kullanmayı öğretti ama ekok bu sayılarda çok uzun zaman alıyor bunu başka türlü yapabilme şansımız varmı?
Defterimde √3².3².19=9√19 olarak bulunmuş burayı bende yapabilirim ama durumu buraya getirmek zor geliyor bana nasıl yapacagımı bilmiyorum ayrıca 19 sayısını nerden bulmuş ? bu sorduğum soruları bana ayrıntılı anlatabilirmisiniz?
Böyle yüksek sayıların köklerini bulmak için öğretmen ekok kullanmayı öğretti ama ekok bu sayılarda çok uzun zaman alıyor bunu başka türlü yapabilme şansımız varmı?
Defterimde √3².3².19=9√19 olarak bulunmuş burayı bende yapabilirim ama durumu buraya getirmek zor geliyor bana nasıl yapacagımı bilmiyorum ayrıca 19 sayısını nerden bulmuş ? bu sorduğum soruları bana ayrıntılı anlatabilirmisiniz?
gereksizyorumcu 01:15 19 Eki 2012 #10
ekokla sonuç rasyonel değilse numerik değer bulamazsınız, ya da ne bileyim size derki √19=4,375 alınız , siz de sonuçta buuduğunuz √19 un yerine bunu yazarak numerik değer bulrsunuz.
bizim yukarıda yazdığımız yolda ise √19 un yaklaşık değerini bilmeye gerek olmaksızın bu sayıyı yaklaşık olarak hesaplıyoruz
1539 a en yakın kare 1521=39² öyleyse bu sayı da 39+(1539-1521)/78~39,23 e oldukça yakındır
bizim yukarıda yazdığımız yolda ise √19 un yaklaşık değerini bilmeye gerek olmaksızın bu sayıyı yaklaşık olarak hesaplıyoruz
1539 a en yakın kare 1521=39² öyleyse bu sayı da 39+(1539-1521)/78~39,23 e oldukça yakındır