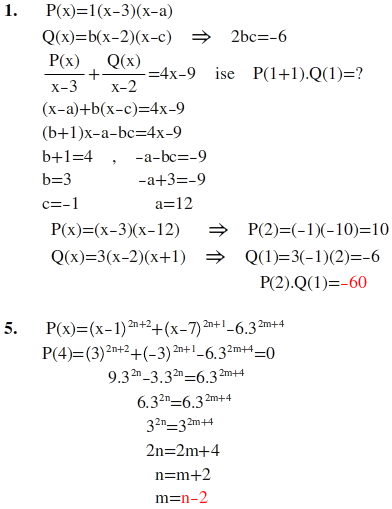polinomlar

1) P(x), (x-3) ile tam bölünebilen ve baş katsayısı 1 olan ikinci dereceden bir polinomdur. Q(x), (x-2) ile tam bölünebilen ve sabit terimi (-6) olan ikinci dereceden bir polinomdur.

P(x)/x-3 + Q(x)/x-2 = 4x-9 olduğuna göre, P(x+1).Q(x) polinomunun katsayılar toplamı kaçtır? cevap: -60

2) 3. dereceden bir P(x) polinomunun (x-1), (x-2) ve (x+2) ile bölümünden kalanlar birbirine eşit ve 5 tir.

P(x+1) polinomunun (x-2) ile bölümünden kalan 25 olduğuna göre, P(x) polinomunun sabit terimi kaçtır? cevap:13


3) P(x) polinomunun (x+2) ile bölümünden kalan (-2) ve (x-2) ile bölümünden kalan -4 tür.

[P(x²)] polinomunun (x²-4) ile bölümünden kalanı yazınız. cevap: 3x+10


4) P(x) bir polinom olmak üzere,
P(x-7)+P(x-6)+...+P(x+8)=16x+8 olduğuna göre, P(x-4) polinomunun (x-8) ile bölümünden kalan kaçtır? cevap:4


5) n ve m birer doğal sayı olmak üzere,

P(x)= (x-1)²ⁿ⁺² + (x-7)²ⁿ⁺¹ - 6.3^2m+4

polinomu (x-4) ile tam bölünebildiğine göre, m nin n cinsinden eşiti nedir? cevap: n-2

C-2
P(x)=a.(x-1).(x-2).(x+2)+5
P(3)=25 verilmiş.
P(3)=a.(-2).(-1).5+5=25
10a=20 , a=2 bulunur.
P(0) isteniyor yerine yazalım,
P(0)=2.(-1).(-2).(2)+5
P(0)=13 bulunur.

C-3
Gece gece uzun uzun işlem yapmayayım.
İlk öncelikle P(x) ile bölümünden kalanı bulun daha sonra x gördüğünüz yere x² yazarak P(x²) ile bölümünden kalanı bulabilirsin.

c-4
Bu soruyu kısa bir süre önce çözdüğümüze eminim,
P(x)=mx+n olsun.
P(x-7)=mx-7m+n olacaktır.
P(x-6)=mx-6m+n olacaktır.
Bu şekilde P(x+7)'ye kadar olan terimleri toplayın , daha sonra P(x)'i de ekleyip 16x+8'e eşitleyin.
Önemli olan sadeleştirmeleri görmek.