1. sorum: -6(sin5+icos5) in kutupsal biçim ?
2. sorum : z1=5(sin40+icos40)
z2=4(sin160+isin40)
arg(z1)+arg(z2) :=?
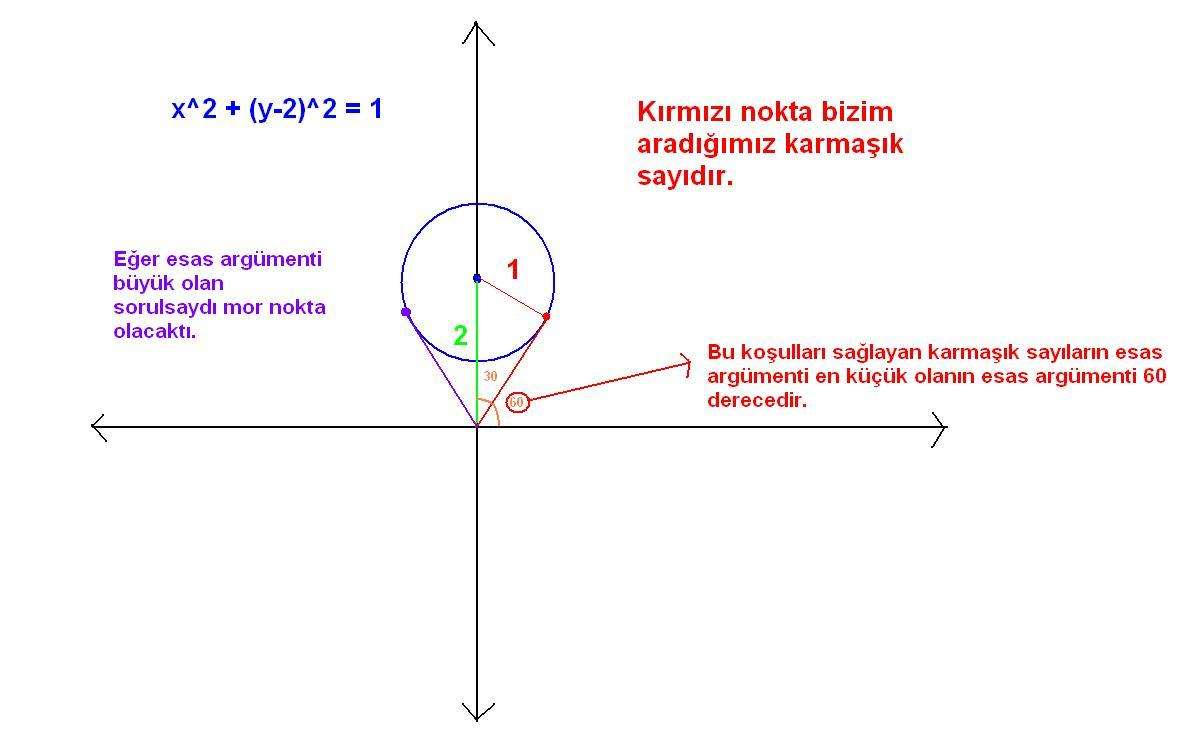
3.sorum: |z-2i|=1 eşitliğini sağlayan z karmaşık sayılarından esas argümenti en küçük olanın esas argümenti kaçtır?
4.sorum: |z-3+4i=2 eşitliğin sağlayan z karmaşık sayısı içinesas argümenti en büyük olanının modülü?
5.sorum: z1=3cis20
z2=3cis160 ise z1-z2=?
2. sorum : z1=5(sin40+icos40)
z2=4(sin160+isin40)
arg(z1)+arg(z2) :=?
3.sorum: |z-2i|=1 eşitliğini sağlayan z karmaşık sayılarından esas argümenti en küçük olanın esas argümenti kaçtır?
4.sorum: |z-3+4i=2 eşitliğin sağlayan z karmaşık sayısı içinesas argümenti en büyük olanının modülü?
5.sorum: z1=3cis20
z2=3cis160 ise z1-z2=?
C.1-6.(sin5+icos5)=6.(-sin5-icos5)=6.(-cos85-isin85)=6.(cos265+isin265)=6cis265
Unutmadıysam eğer
Unutmadıysam eğer
C-3:
z = x+iy olsun:
|z-2i| = 1
|x+(y-2)i| = 1
x² + (y-2)2 = 1
Sorulan sayı merkezi (0,2) yarıçapı 1 br olan çember üzerindedir:

z = x+iy olsun:
|z-2i| = 1
|x+(y-2)i| = 1
x² + (y-2)2 = 1
Sorulan sayı merkezi (0,2) yarıçapı 1 br olan çember üzerindedir:
C-1 doğru.
4. sorunun cevabı √21 mi?
4. sorunun cevabı √21 mi?
evet 4.sorunun cevabı √21
2.soruyu ve 5.yi nasıl yapıcaz:? teşkekürler herkese ...
2.soruyu ve 5.yi nasıl yapıcaz:? teşkekürler herkese ...
C-4:
Bu soruyu da 3. sorudaki gibi çözüyoruz:
z = x+iy
|z-3+4i| = 2
|(x-3) + (y+4)i| = 2
(x-3)2 + (y+4)2 = 4
Bu da merkezi (3,-4) yarıçapı 2 br olan çemberdir:

OMT üçgeninde pisagor yapılırsa |z|=√21 bulunur.
-------------------------
2. sorunda z2 ' yi düzenlemeyi bir türlü başaramadım. Son soruda da dönüşüm formülleri uygulanarak çözüme ulaşılabilir. Onların da cevaplarını yazarsan iyi olur.
Bu soruyu da 3. sorudaki gibi çözüyoruz:
z = x+iy
|z-3+4i| = 2
|(x-3) + (y+4)i| = 2
(x-3)2 + (y+4)2 = 4
Bu da merkezi (3,-4) yarıçapı 2 br olan çemberdir:

OMT üçgeninde pisagor yapılırsa |z|=√21 bulunur.
-------------------------
2. sorunda z2 ' yi düzenlemeyi bir türlü başaramadım. Son soruda da dönüşüm formülleri uygulanarak çözüme ulaşılabilir. Onların da cevaplarını yazarsan iyi olur.
[QUOTE=istersen;82091]
2. sorum : z1=5(sin40+icos40)
z2=4(sin160+icos40)
arg(z1)+arg(z2) :=? soruyu yanlış yazmışım afedesiniz... cevap:120
5. sorunun cevabı ise 6sin70
2. sorum : z1=5(sin40+icos40)
z2=4(sin160+icos40)
arg(z1)+arg(z2) :=? soruyu yanlış yazmışım afedesiniz... cevap:120
5. sorunun cevabı ise 6sin70
C-5:
3cis20-3cis160
3(cos20+i.sin20-cos160-i.sin160)
3.((cos20-cos160)+i.(sin20-sin160))
3.((-2sin90.sin(-70))+i.(2cos90.sin(-70)))
3.(-2sin(-70))
3.2sin70
6.sin70
3cis20-3cis160
3(cos20+i.sin20-cos160-i.sin160)
3.((cos20-cos160)+i.(sin20-sin160))
3.((-2sin90.sin(-70))+i.(2cos90.sin(-70)))
3.(-2sin(-70))
3.2sin70
6.sin70
