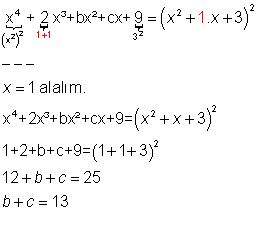1) P(x) bir polinom olmak üzere
x².P(x)= x³+3x²-(a+4)x+b-6 bağıntısı veriliyor. Buna göre P(ax+b) polinomunun katsayılar toplamı kaçtır?
-----------------------------------
2) P(x)= x²+2ax-5
Q(x)=3x+b
p(3x)= Q(3x²+2x) olduğuna göre P(1)+Q(1) kaçtır?
------------------------------------------
3) P(x)=x³+ax²+bx+c polinomu (x-1)³ ile tam bölünebiliyorsa a.b.c kaçtır?
-----------------------------------------
4) Pozitif katsayılı P(x) polinomu,
P(x).P(3x)=3x²+4x+1 koşulunu sağlıyorsa P(-1) kaçtır?
-------------------------------------------
5) P(x), pozitif katsayılı bir polinomdur.
x⁴+2x³+bx²+cx+9=[P(x)]² olduğuna göre b+c kaçtır?
x².P(x)= x³+3x²-(a+4)x+b-6 bağıntısı veriliyor. Buna göre P(ax+b) polinomunun katsayılar toplamı kaçtır?
-----------------------------------
2) P(x)= x²+2ax-5
Q(x)=3x+b
p(3x)= Q(3x²+2x) olduğuna göre P(1)+Q(1) kaçtır?
------------------------------------------
3) P(x)=x³+ax²+bx+c polinomu (x-1)³ ile tam bölünebiliyorsa a.b.c kaçtır?
-----------------------------------------
4) Pozitif katsayılı P(x) polinomu,
P(x).P(3x)=3x²+4x+1 koşulunu sağlıyorsa P(-1) kaçtır?
-------------------------------------------
5) P(x), pozitif katsayılı bir polinomdur.
x⁴+2x³+bx²+cx+9=[P(x)]² olduğuna göre b+c kaçtır?
C.1
P(x) polinom olduğundan ifadede 2.dereceden küçük terimler olmamalıdır bu nedenle
a+4=0 , a=-4 , b-6=0 , b=6 bulunur.
p(-4x+6)'nın katsayılar toplamı P(2)'dir.
x².P(x)=x³+3x²
4.P(2)=8+12
4.P(2)=20
P(2)=5
P(x) polinom olduğundan ifadede 2.dereceden küçük terimler olmamalıdır bu nedenle
a+4=0 , a=-4 , b-6=0 , b=6 bulunur.
p(-4x+6)'nın katsayılar toplamı P(2)'dir.
x².P(x)=x³+3x²
4.P(2)=8+12
4.P(2)=20
P(2)=5
C.2
P(3x)=9x²+6ax-5
Q(3x²+2x)=3.(3x²+2x)+b => 9x²+6x+b şeklindedir.
9x²+6ax-5 = 9x²+6x+b
a=1 bulunur. b=-5 bulunur.Burdan sonrasını halledersin zaten.
P(3x)=9x²+6ax-5
Q(3x²+2x)=3.(3x²+2x)+b => 9x²+6x+b şeklindedir.
9x²+6ax-5 = 9x²+6x+b
a=1 bulunur. b=-5 bulunur.Burdan sonrasını halledersin zaten.
C.4
P(x)=mx+n
P(3x)=3mx+n şeklindedir.
(mx+n)*(3mx+n)=3x²+4x+1
m=1 , n=1 olur.Sonrası
P(x)=x+1
P(-1)=0
P(x)=mx+n
P(3x)=3mx+n şeklindedir.
(mx+n)*(3mx+n)=3x²+4x+1
m=1 , n=1 olur.Sonrası
P(x)=x+1
P(-1)=0
C.3
(x-1)³ ile tam bölünüyorsa P(1)=0 , P'(1)=0 (1.türev) , P''(1)=0 olmalı (2.türev)
Türev bilirseniz kısa olur
P(1)=0 olmalı => 1+a+b+c = 0
P'(x)=3x²+2ax+b , P'(1)=0 , => 3+2a+b= 0
P''(x)=>6x+2a => P''(2)=0 , => P''(2)=12+2a=0 , 2a=-12 , a=-6 bundan sonrasını bulursun zaten denklem çözer gibi.
(x-1)³ ile tam bölünüyorsa P(1)=0 , P'(1)=0 (1.türev) , P''(1)=0 olmalı (2.türev)
Türev bilirseniz kısa olur
P(1)=0 olmalı => 1+a+b+c = 0
P'(x)=3x²+2ax+b , P'(1)=0 , => 3+2a+b= 0
P''(x)=>6x+2a => P''(2)=0 , => P''(2)=12+2a=0 , 2a=-12 , a=-6 bundan sonrasını bulursun zaten denklem çözer gibi.
5. sorunun kısa yolu yok herhalde p(x)=ax²+bx+c dicen bunun karesini alıp diğer denkleme eşitlicen ama kısa yolu varsa bilmem