-Polinomlar-

S.1

P(x)=ax¹⁵+bx⁹-3
polinomunun çarpanlarından biri x³+1 dir.
Buna göre, P(x) polinomunun x²+1 ile bölümünden kalan aşağıdakilerden hangisidir ? C.(3x-3)

Şöyle mantık yürüttüm:
P(x)=(x+1).(x²-x+1).(ax⁵+........)
P(x) polinomunun x²+1 ile bölümünden kalanı bulmak için x² yerine -1 yazalım.
P(x)=(1-x).(ax⁵+........)
Bu durumda cevap şıklardan sadece 3x-3 olabilir. Ancak hangisi olabilir demediği için kesin bir çözümü vardır diye umuyorum.

S.2

P(x)=axⁿ⁺¹+bxⁿ+1 polinomunun çarpanlarından biri x²-2x+1 olduğuna göre, a kaçtır ? C.(a=n)

S.3

P(ax)=x⁴+ax+b
P(bx)=x⁴+bx+a
P(a)=5
olduğuna göre, P(-2) kaçtır ? C.(1)

S.4

n doğal sayıdır.
P(x)=x⁴ⁿ-5x²ⁿ⁺¹+4x-6
polinomunun x³-x ile bölümünden kalan R(x) olduğuna göre, R(x) polinomunun x-3 ile bölümünden kalan kaçtır ?
C.(6)

Şöyle mantık yürüttüm:
P(x)=x.(x+1).(x-1).Q(x)+R(x)
R(x) max 2. dereceden bir fonksiyon olabilir.
R(x)=ax²+bx+c
P(0)=-6
c=-6
P(1)=-6
a+b+c=-6
a+b=0
P(-1)=-4
a-b+c=-4
a-b=2
a=1
b=-1
ax²+bx+c=x²-x-6
R(3)=9-3-6=0
0 buluyorum ancak cevap 6 imiş.

3)
İlk polinomda P(0) = b
İkinci polinomda P(0) = a
o zaman a = b

İlk polinomda x = 1 için P(a) = 1 + a + b
a + b + 1 = 5, ve a = b'den a ve b 2 çıkar.
P(2x) = x^4 + 2x + 2
x = -1 için P(-2) = 1

4)
Seninle aynı sonucu buldum

2)
P(x)=axⁿ⁺¹+bxⁿ+1 polinomunun çarpanlarından biri x²-2x+1 olduğuna göre, a kaçtır ? C.(a=n)
x²-2x+1=(x-1)²
P(1)=a+b+1=0, a+b=-1
P'(1)=(n+1).a.xⁿ+b.n.x^n-1=0
P'(1)=(a+b).n+a=0
P'(1)=-n+a=0
a=n

3)
P(ax)=x⁴+ax+b
P(bx)=x⁴+bx+a
P(a)=5
olduğuna göre, P(-2) kaçtır ? C.(1)
P(a)=1+a+b=5
a+b=4
P(a.b)=b⁴+a.b+b
P(b.a)=a⁴+b.a+a
b⁴+a.b+b=a⁴+a.b+a
b⁴+b=a⁴+a
b=a=2
P(2.-1)=1-2+2=1

4. sorunun çözümünde bir hata göremedim. Sorular hangi kaynaktan?

1)

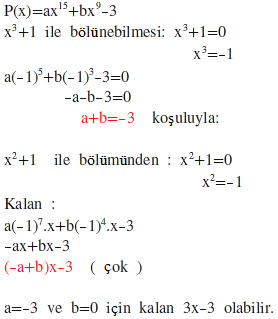
slymnoymak hocam, frk ve ceday çözümler için teşekkür ederim. Elinize,emeğinize sağlık...
Sorular karekök yayınlarından.**

frk, soru 2'de türev kısmını anlayamadım ama, kurcalamayayım mı...

P(-1)= neden (-4) oldu?

4. soruda r(x) inasıl max 2. dereceden kabul ediyorsun bn anlamadım burayı?

n doğal sayı denmiş, -1'in çift kuvvetleri +1, tek kuvvetleri yine -1 olacak
x yerine -1 yazınca (-1)^4 -5(-1)^5 + 4(-1) - 6
1 + 5 - 4 - 6
P(-1) = -4

Kalanın derecesi bölümden küçük olacağı için R(x)'in derecesi en fazla 2 olabilir.

R(x) kalan ve bölenden küçük olmak zorunda olduğu için, daha küçük dereceli bir ifade olmak zorunda, sebebindendir diye düşünüyorum... 3. dereceden olursa bölenden büyük olabilir...