10 kenarlı bir düzgün cokgenin köşegen sayısı kactır?
c(10,2) olması gerekmiyormu ?
yardım ederseniz sevinirim..
c(10,2) olması gerekmiyormu ?
yardım ederseniz sevinirim..
köşegen sayısı
n.(n-3)/2
10.7/2=35 olmuyor muydu, doğru hatırlıyor muyum?
n.(n-3)/2
10.7/2=35 olmuyor muydu, doğru hatırlıyor muyum?
10 kenarlı bir düzgün cokgenin köşegen sayısı kactır?
c(10,2) olması gerekmiyormu ?
yardım ederseniz sevinirim..
c(10,2) olması gerekmiyormu ?
yardım ederseniz sevinirim..
bu sayıdan n çıkarırsan sonucu elde edebilirsin
kenarların birleşimini saymış olmuyormuyum ? n(kenar sayısını) cıkarma sebepini tam olarak anlayamadım..yardımcı olursanız sevinirim..
soru 1:
1 yüksek okulda 8 dersten 2 si aynı saatte,3 ü bunlardan farklı birbirleriyle aynı başka bir saatte verilmektedir.digerlerin saaatleri bunlardan ve birbirlerinden farklıdır.
buna göre bu ögrenci 8 dersten 3 tanesini kac degişik şekilde secebilir?
soru 2 :
Bir sınıftan secilen 7 ögrenci,iki gruba ayrılıyor bu iki gruptan biris istanbula ötekide Ankaraya gönderiliyor.
her iki şehire de en az birer ögrenci gönderilecegine göre,bu iki grup kac degişik şekilde oluşturulabilir?
soru : 3
7 kişi üc arabayla geziye cıkacaklardır.Arabaların birinde 3,diger iikisinde 2 şer kişilik yer bulunmaktadır.
belli iki kişi yanyana gitmemek şartı ile en fazla kac farklı şekilde gidilebilir?
soru 4:
30 kişilik bir sınıfın 2/15 'i sadece futbol ,3/10 u sadece basketbol oynamaktadır.
bu sınıftan futbol ve basketbol oynayan en cok kac farklı ögrenci grubu oluşturulabilir?
yardımcı olursanız sevinirim..
kolay gelsin..
1 yüksek okulda 8 dersten 2 si aynı saatte,3 ü bunlardan farklı birbirleriyle aynı başka bir saatte verilmektedir.digerlerin saaatleri bunlardan ve birbirlerinden farklıdır.
buna göre bu ögrenci 8 dersten 3 tanesini kac degişik şekilde secebilir?
soru 2 :
Bir sınıftan secilen 7 ögrenci,iki gruba ayrılıyor bu iki gruptan biris istanbula ötekide Ankaraya gönderiliyor.
her iki şehire de en az birer ögrenci gönderilecegine göre,bu iki grup kac degişik şekilde oluşturulabilir?
soru : 3
7 kişi üc arabayla geziye cıkacaklardır.Arabaların birinde 3,diger iikisinde 2 şer kişilik yer bulunmaktadır.
belli iki kişi yanyana gitmemek şartı ile en fazla kac farklı şekilde gidilebilir?
soru 4:
30 kişilik bir sınıfın 2/15 'i sadece futbol ,3/10 u sadece basketbol oynamaktadır.
bu sınıftan futbol ve basketbol oynayan en cok kac farklı ögrenci grubu oluşturulabilir?
yardımcı olursanız sevinirim..
kolay gelsin..
C.1

8 dersten 3ünü;
i)Saat 14:00da olan derslerden 1ini, Saat 16:00da olan derslerden birini ve H,J,İ derslerinden birini seçsin
C(2,1).C(3,1).C(3,1)=2.3.3=18
ii)Saat 14:00da olan derslerden 1ini,ve H,J,İ derslerinden ikisini seçsin
C(2,1).C(3,2)=2.3=6
iii)Saat 16:00da olan derslerden birini ve H,J,İ derslerinden ikisini seçsin.
C(3,1).C(3,2)=3.3=9
iiii)H,J,İ derslerinden hepsini seçsin.
C(3,3)=1
Toplamda:18+6+9+1=34
C.2
A grubu B grubu
C(7,1) . C(6,6) =7
C(7,2) . C(5,5) =21
C(7,3) . C(4,4)=35
C(7,4) . C(3,3) =35
C(7,5) . C(2,2) =21
C(7,6) . C(1,1) =7
Toplamda:126
2.yol:
Tüm durumlardan-(bütün kişilerin aynı grupta olduğu durumlar)
Tüm durumlar=27=128
Bütün kişilerin aynı grupta olduğu durumlar=Bütün kişiler aynı grupta olsun.
Bunlar ya İstanbula gider ya Ankaraya yani 2 durum var.
128-2=126
C.3
Tüm-Belli iki kişinin yanyana gittiği durumlar.
Tüm=C(7,3).C(4,2).C(2,2)=35.6=210
Belirli iki kişinin yanyana gittiği durumlar.
Belirli iki kişiyi 1 kişi kabul edersek;
i)3 kişilik araca yanlarına 1 kişi alarak gitsinler.
C(5,1)=5
Kalan 4 kişi
C(4,2).C(2,2)=6 (6.5=30)
ii)2 kişilik araçtan herhangi birine gitsinler.
C(2,1)=2
Kalan 5 kişi
C(5,3).C(2,2)=10 (2.10)
Tüm=210
Belli iki kişinin yanyana gittiği durumlar=30+20=50
210-50=160
C.4
Sadece futbol oynayan kişi sayısı=4
Sadece basketbol oynayan kişi sayısı=9
Kalan 17 kişi;
C(17,0)+C(17,1)+....C(17,17)=217
C(17,0)=0 kişi basketbol ve futbol oynar.
C(17,1)=1 kişi basketbol ve futbol oynar.
...
C(17,17)=17 kişi basketbol ve futbol oynar.
Cevap:217-1
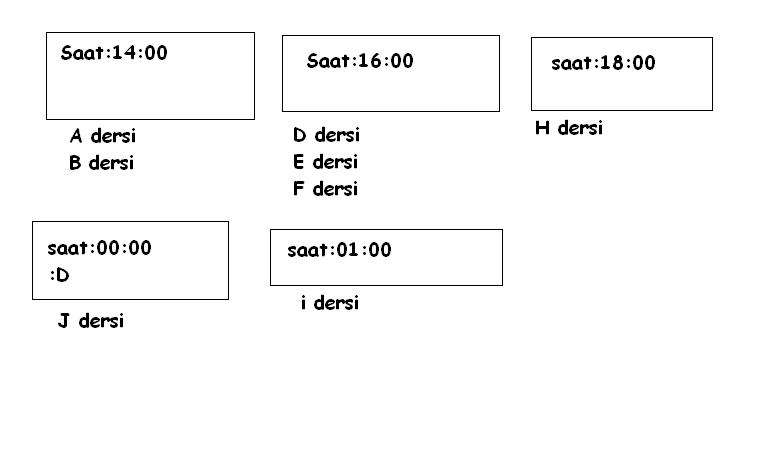
8 dersten 3ünü;
i)Saat 14:00da olan derslerden 1ini, Saat 16:00da olan derslerden birini ve H,J,İ derslerinden birini seçsin
C(2,1).C(3,1).C(3,1)=2.3.3=18
ii)Saat 14:00da olan derslerden 1ini,ve H,J,İ derslerinden ikisini seçsin
C(2,1).C(3,2)=2.3=6
iii)Saat 16:00da olan derslerden birini ve H,J,İ derslerinden ikisini seçsin.
C(3,1).C(3,2)=3.3=9
iiii)H,J,İ derslerinden hepsini seçsin.
C(3,3)=1
Toplamda:18+6+9+1=34
C.2
A grubu B grubu
C(7,1) . C(6,6) =7
C(7,2) . C(5,5) =21
C(7,3) . C(4,4)=35
C(7,4) . C(3,3) =35
C(7,5) . C(2,2) =21
C(7,6) . C(1,1) =7
Toplamda:126
2.yol:
Tüm durumlardan-(bütün kişilerin aynı grupta olduğu durumlar)
Tüm durumlar=27=128
Bütün kişilerin aynı grupta olduğu durumlar=Bütün kişiler aynı grupta olsun.
Bunlar ya İstanbula gider ya Ankaraya yani 2 durum var.
128-2=126
C.3
Tüm-Belli iki kişinin yanyana gittiği durumlar.
Tüm=C(7,3).C(4,2).C(2,2)=35.6=210
Belirli iki kişinin yanyana gittiği durumlar.
Belirli iki kişiyi 1 kişi kabul edersek;
i)3 kişilik araca yanlarına 1 kişi alarak gitsinler.
C(5,1)=5
Kalan 4 kişi
C(4,2).C(2,2)=6 (6.5=30)
ii)2 kişilik araçtan herhangi birine gitsinler.
C(2,1)=2
Kalan 5 kişi
C(5,3).C(2,2)=10 (2.10)
Tüm=210
Belli iki kişinin yanyana gittiği durumlar=30+20=50
210-50=160
C.4
Sadece futbol oynayan kişi sayısı=4
Sadece basketbol oynayan kişi sayısı=9
Kalan 17 kişi;
C(17,0)+C(17,1)+....C(17,17)=217
C(17,0)=0 kişi basketbol ve futbol oynar.
C(17,1)=1 kişi basketbol ve futbol oynar.
...
C(17,17)=17 kişi basketbol ve futbol oynar.
Cevap:217-1
öncelikle yardımın icin teşekkürler..
uyarın icinde teşekkürler..
2.soruyu ben yanlış yazdım galiba cevapı 126 olması gerekiyor ben degişik şekilde oluşturulabiliri,secilebilir diye yazmışım..kusura bakmayın..
basketbol sorusunun cevapıda 2^17-1 bu -1 cıkartmalarının nedeni C(17,0) kombinasyonundan dolayımı ?
tekrardan cok teşekkürler..
uyarın icinde teşekkürler..
2.soruyu ben yanlış yazdım galiba cevapı 126 olması gerekiyor ben degişik şekilde oluşturulabiliri,secilebilir diye yazmışım..kusura bakmayın..
basketbol sorusunun cevapıda 2^17-1 bu -1 cıkartmalarının nedeni C(17,0) kombinasyonundan dolayımı ?
tekrardan cok teşekkürler..
öncelikle yardımın icin teşekkürler..
uyarın icinde teşekkürler..
2.soruyu ben yanlış yazdım galiba cevapı 126 olması gerekiyor ben degişik şekilde oluşturulabiliri,secilebilir diye yazmışım..kusura bakmayın..
Evet futbol ve basketbol oynayan en az bir kişi olmalıymış.
0 kişi olmasını çıkarırız bu durumda.
basketbol sorusunun cevapıda 2^17-1 bu -1 cıkartmalarının nedeni C(17,0) kombinasyonundan dolayımı ?
tekrardan cok teşekkürler..
uyarın icinde teşekkürler..
2.soruyu ben yanlış yazdım galiba cevapı 126 olması gerekiyor ben degişik şekilde oluşturulabiliri,secilebilir diye yazmışım..kusura bakmayın..
Evet futbol ve basketbol oynayan en az bir kişi olmalıymış.
0 kişi olmasını çıkarırız bu durumda.
basketbol sorusunun cevapıda 2^17-1 bu -1 cıkartmalarının nedeni C(17,0) kombinasyonundan dolayımı ?
tekrardan cok teşekkürler..
