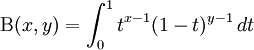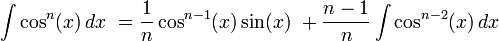olduğunu gösteriniz
binom açılımı yapıp ifadeyi açtım integralini alıp yerine sınır değerlerini koydum işlem hatam yoksa çok yaklaştım (tabi bu yol doğruysa) ancak bir türlü paydayı eşitleyip ifadeyi düzenleyemedim yardımcı olabilirseniz çok sevinirim

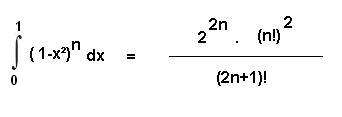 olduğunu gösteriniz
olduğunu gösteriniz