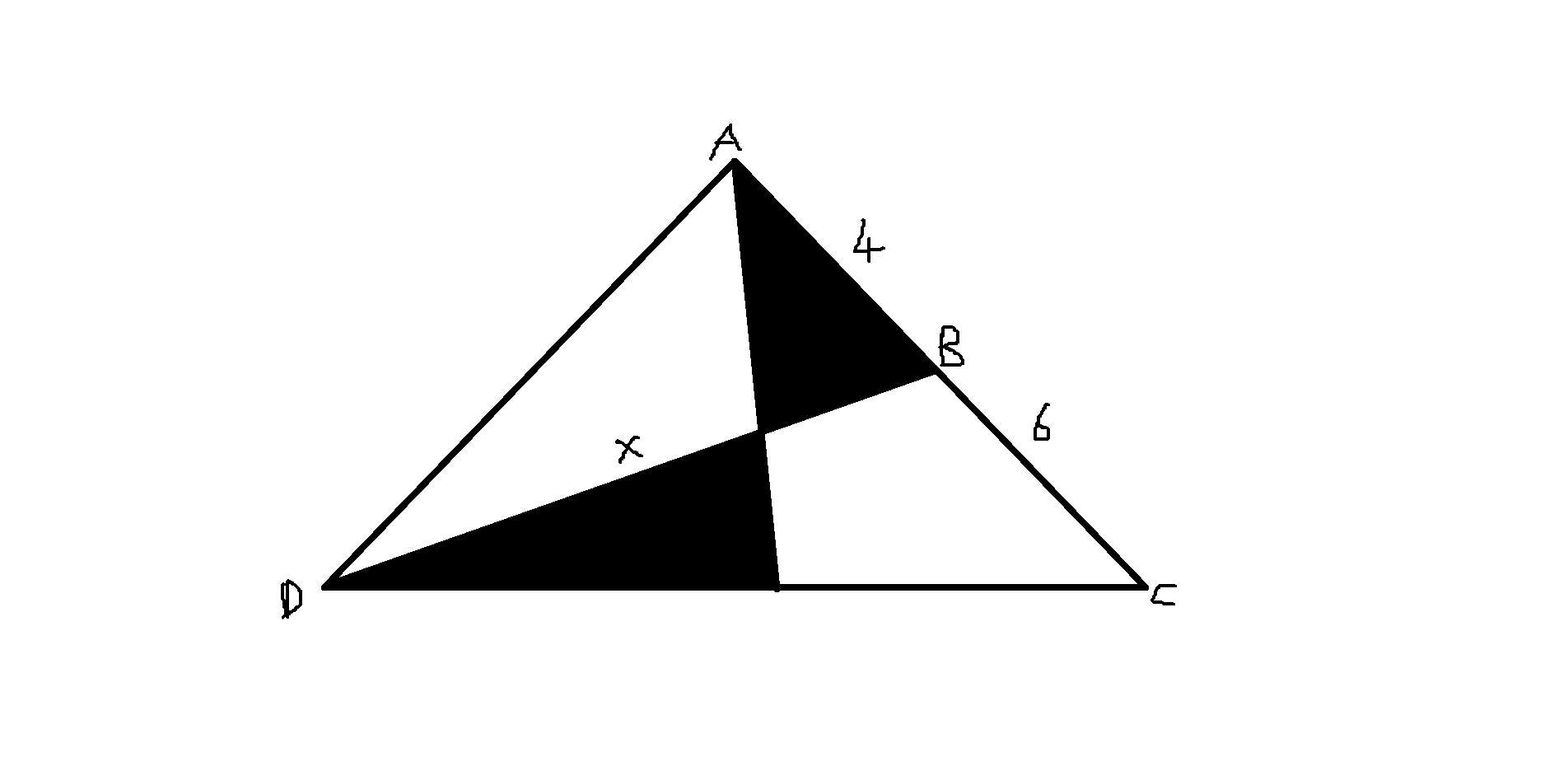
taralı alanlar eşit x=?
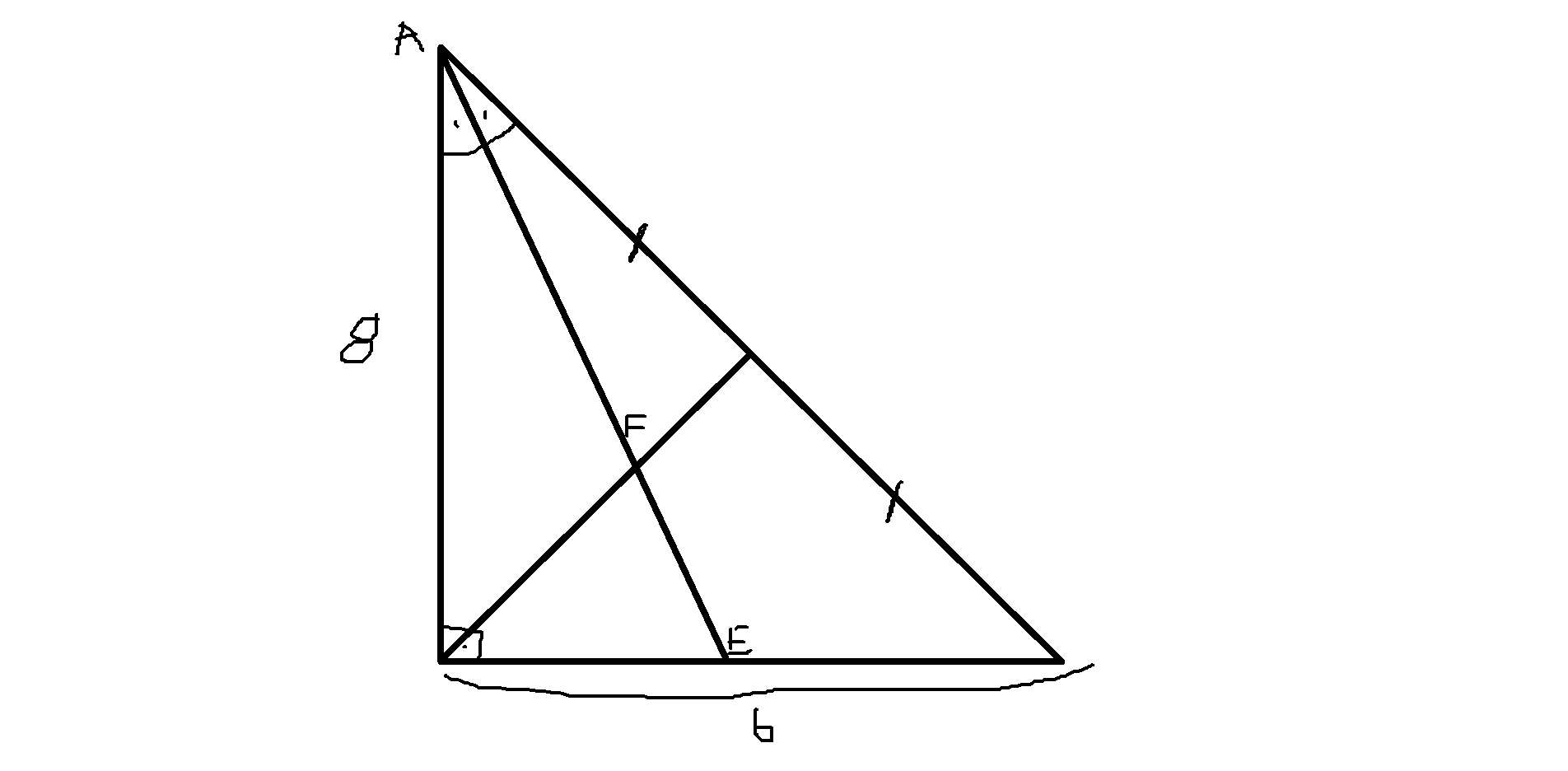
AF/FE ORANI=?
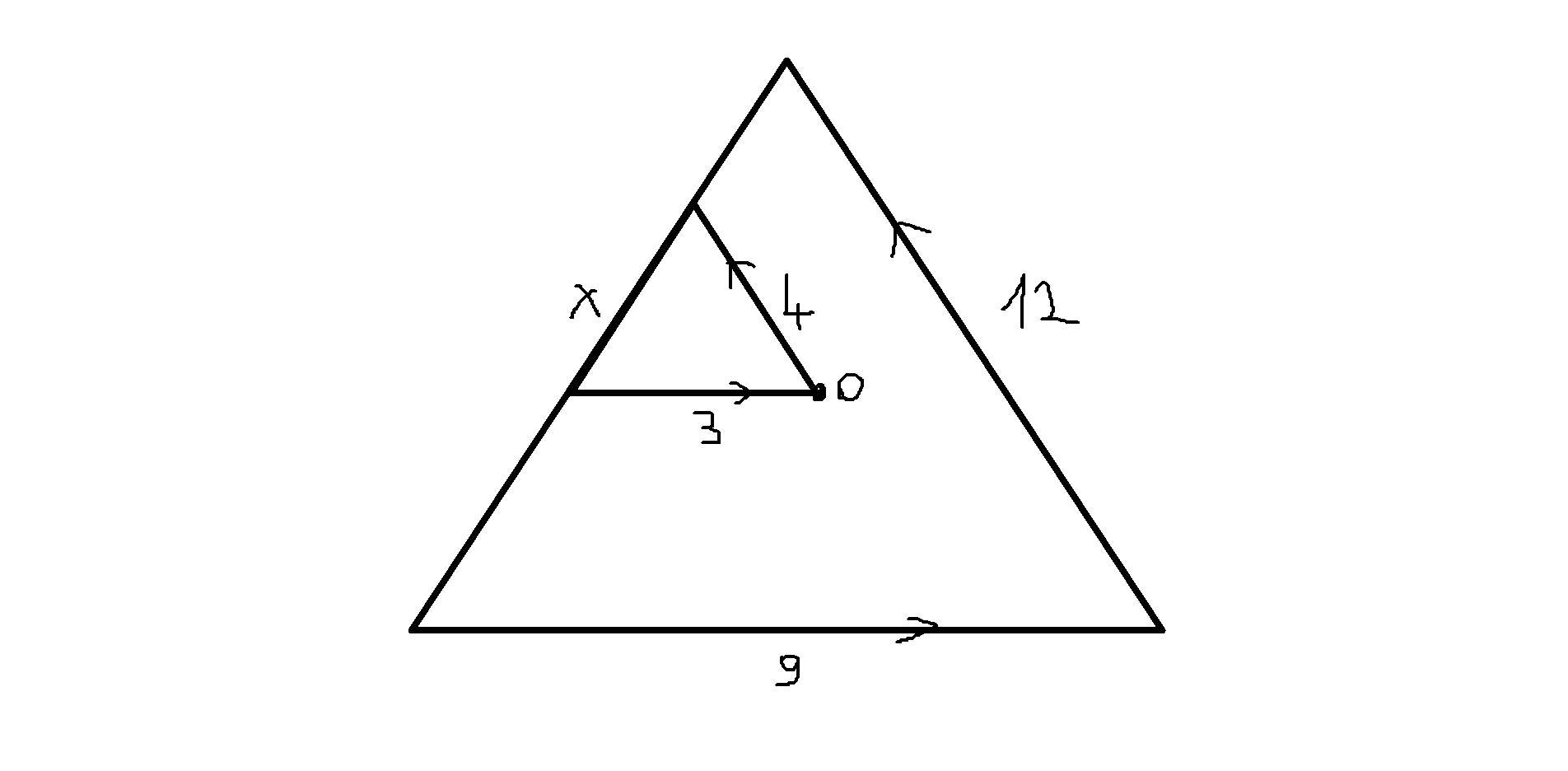
O iç teğet çemberin merkezi x=?
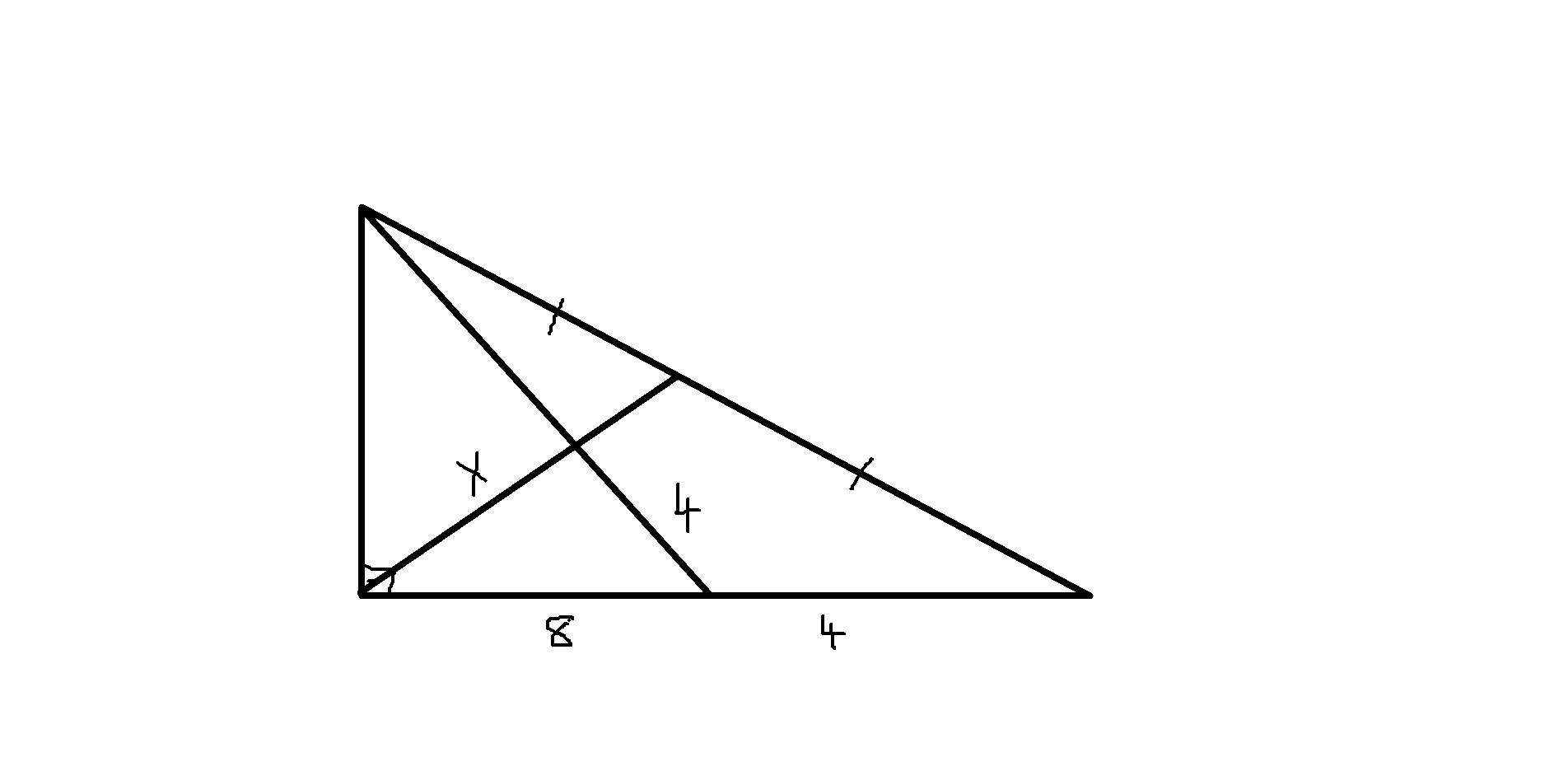
x=?
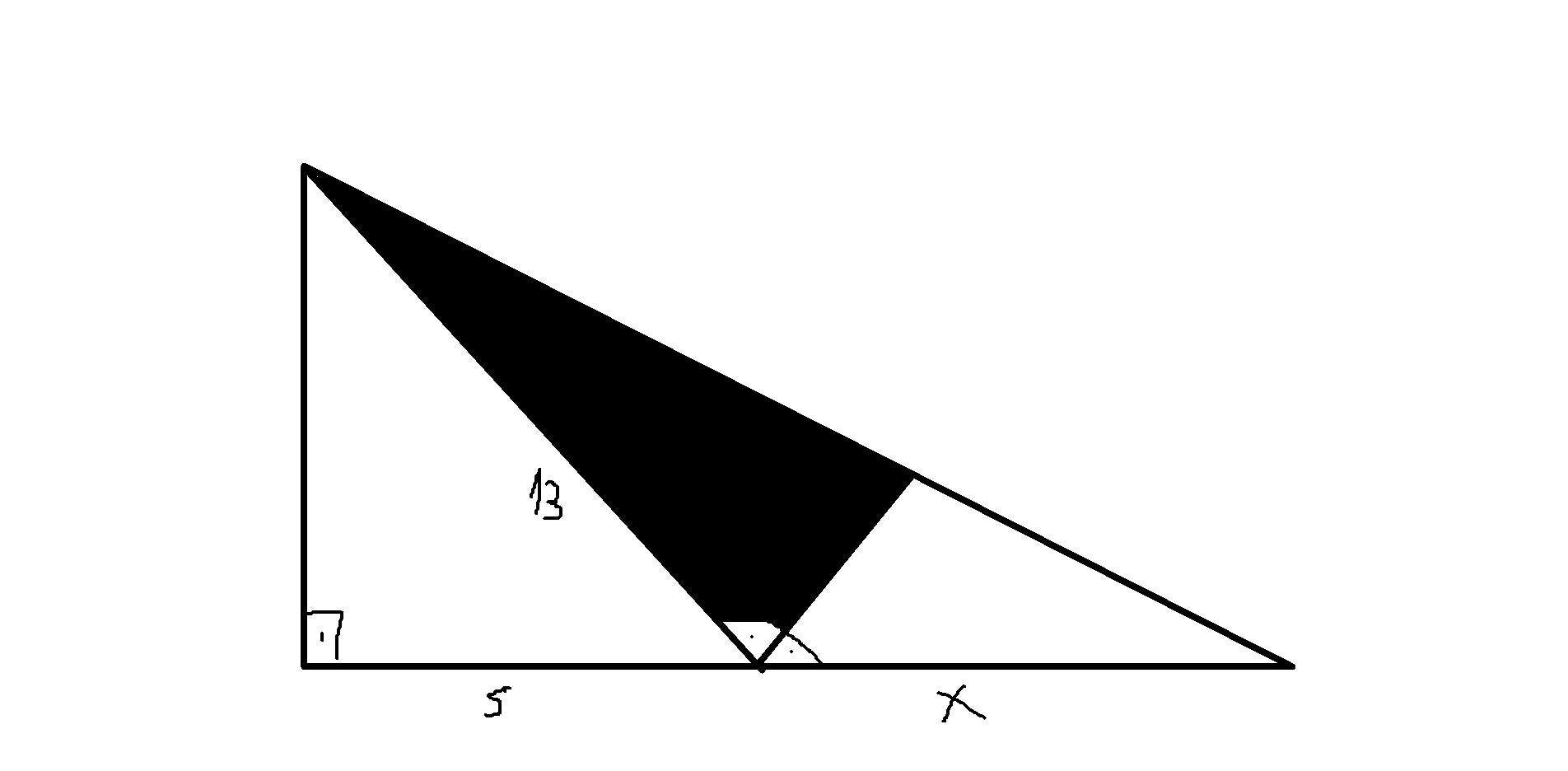
taralı alan 26 x=?
svsmumcu26 20:06 20 Haz 2013 #2
2.
Eşit parçaların her birinin 5er birim olduğunu biliyoruz.
O dik üçgenin en alt köşesine D noktası diyelim.
ve en sağ köşe de c olsun.
|DE|/|CE|=4/5 , |DE|=4K , |CE|=5K'dır.
9k=6 , k=2/3 bulunur.
O halde |DE|=8/3 , |CE|=10/3 bulunur.
Şimdi menelaus uygulayalım.
6/3/6 . 5/5 . |AF|/|FE|=1 olmalıdır.
12.|AF|/|FE|=1
|AF|/|FE|=1/12 bulunur.
Eşit parçaların her birinin 5er birim olduğunu biliyoruz.
O dik üçgenin en alt köşesine D noktası diyelim.
ve en sağ köşe de c olsun.
|DE|/|CE|=4/5 , |DE|=4K , |CE|=5K'dır.
9k=6 , k=2/3 bulunur.
O halde |DE|=8/3 , |CE|=10/3 bulunur.
Şimdi menelaus uygulayalım.
6/3/6 . 5/5 . |AF|/|FE|=1 olmalıdır.
12.|AF|/|FE|=1
|AF|/|FE|=1/12 bulunur.
svsmumcu26 20:12 20 Haz 2013 #3
5.
Burada tüm üçgenin alanını bulalım.
(x+5).6 => 6x+30 bulunur.
Dik üçgenin alanı 12.5/2 = 30 bulunur o halde sag üçgenin alanı 6x olmalıdır.
26+2x=6x
26=4x
x=13/2 bulunur.
Dipnot:Umarım islem hatası falan yapmamışımdır telden bu kadar bakabildim.Temel mantıklar böyle.
Burada tüm üçgenin alanını bulalım.
(x+5).6 => 6x+30 bulunur.
Dik üçgenin alanı 12.5/2 = 30 bulunur o halde sag üçgenin alanı 6x olmalıdır.
26+2x=6x
26=4x
x=13/2 bulunur.
Dipnot:Umarım islem hatası falan yapmamışımdır telden bu kadar bakabildim.Temel mantıklar böyle.
svsmumcu26 12:23 21 Haz 2013 #4
4.
Menelaus uygularsak o ortadaki uzunluk 4 birim olduğundan menelaus gereği
8/12.1/1.y/4 => 2/3.y/4 => y/6=1 , y=6 bulunur.
O halde dik üçgenin diğer dik kenarı 6-8-10 üçgeni gereği 6 birim bulunur.
Şimdi de üçgenin en sağ tepesinden menelaus uygulayalım. 1/2 . 4/8.x/k (x'in devamı k olsun) = x/4k=1 , x=4k bulunur.Sağ devamı da k olur.
Şimdi 6-12-şeklinde dik üçgen oluştuğundan pisagor teoremi gereği hipotenüs uzunluğu √9.20 = 6√5 bulunur.
Yarı yarıya böldüğünden 3√5'er birim böler.
Görüldüğü gibi 6-12-6√5 dik üçgeni oluştu artık burada ortadan inen kenar ortayın boyu 5k olduğundan kenarortay teoremiyle k çekilip 4k bulursanız x'e ulaşmış olursunuz.(Bu kısmı da biraz işlem olduğundan size bırakıyorum.)
Dipnot.Stewart da iş görmez değil.
Menelaus uygularsak o ortadaki uzunluk 4 birim olduğundan menelaus gereği
8/12.1/1.y/4 => 2/3.y/4 => y/6=1 , y=6 bulunur.
O halde dik üçgenin diğer dik kenarı 6-8-10 üçgeni gereği 6 birim bulunur.
Şimdi de üçgenin en sağ tepesinden menelaus uygulayalım. 1/2 . 4/8.x/k (x'in devamı k olsun) = x/4k=1 , x=4k bulunur.Sağ devamı da k olur.
Şimdi 6-12-şeklinde dik üçgen oluştuğundan pisagor teoremi gereği hipotenüs uzunluğu √9.20 = 6√5 bulunur.
Yarı yarıya böldüğünden 3√5'er birim böler.
Görüldüğü gibi 6-12-6√5 dik üçgeni oluştu artık burada ortadan inen kenar ortayın boyu 5k olduğundan kenarortay teoremiyle k çekilip 4k bulursanız x'e ulaşmış olursunuz.(Bu kısmı da biraz işlem olduğundan size bırakıyorum.)
Dipnot.Stewart da iş görmez değil.
cengizhanhck 23:18 22 Haz 2013 #5
3)
iç teğet çember iç açiortaylarin kesisim noktasidir.O halde açiortaylarimiz çekip paralellikten faydalandiğimizda iki tane ikizkener üçgen olustugunu görürüz.Bu üçgenler benzer olduklarindan dolayi 12/4=9/3=(7+x)/x=3 3x=7+x 2x=7 x=7/2 olur
iç teğet çember iç açiortaylarin kesisim noktasidir.O halde açiortaylarimiz çekip paralellikten faydalandiğimizda iki tane ikizkener üçgen olustugunu görürüz.Bu üçgenler benzer olduklarindan dolayi 12/4=9/3=(7+x)/x=3 3x=7+x 2x=7 x=7/2 olur
cengizhanhck 23:53 22 Haz 2013 #6
1)biraz ilerledim fakat bir türlü bulamadim.Belki diğer arkadaşlar bulabilir veya bir eksiklik olabilir.
svsmumcu26 23:58 22 Haz 2013 #7
Ben de buraya kadar geldim.Yemeğe gidiyorum,çıkmam gerekiyor.Bundan sonra benzerlikten çıkacak gibi.
Dipnot.|DF| ile |FG|nin yerleri ters yazılmıştır.
Dipnot.|DF| ile |FG|nin yerleri ters yazılmıştır.
vazgeçtim değil.