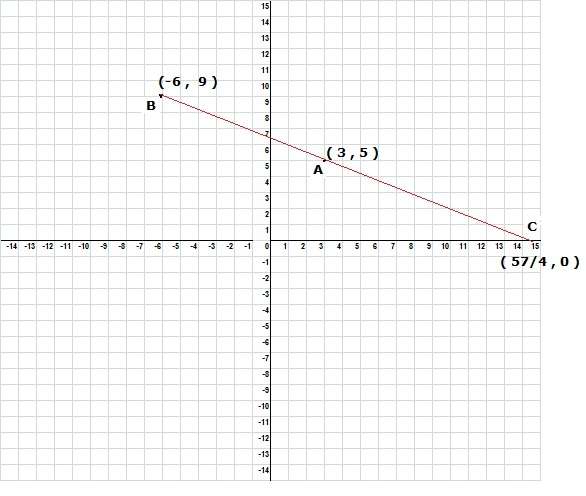
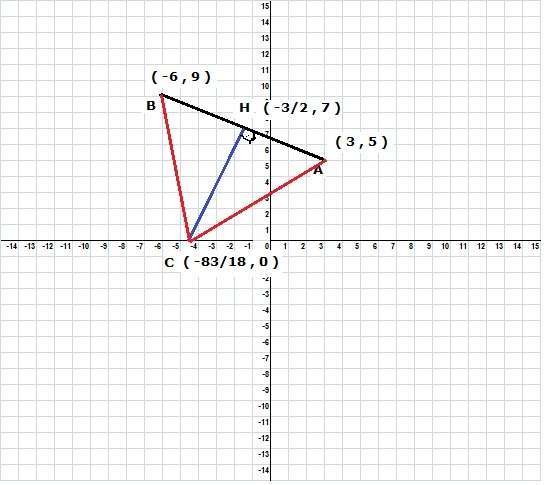
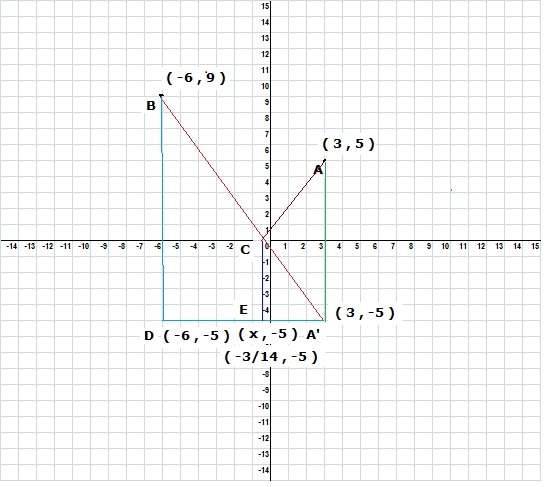
1_ A(1.2) B(3,5) C(x,0) noktaları veriliyor.IıACı-ıBCIı İFADESİNİN EN BÜYÜK OLMASI İÇİN X DEGERİ? (-1/3)
2_ A(-2,6) B(1,4) C(x,0) noktaları veriliyor.IıACı-ıBCIı İFADESİNİN EN KÜÇÜK OLMASI İÇİN X DEGERİ? (-23/6)
3_ A(1,3) B(-4,5) C(0,y) noktaları veriliyorIıACı+ıBCI İFADESİNİN EN küçük OLMASI İÇİN y DEGERİ? (17/5)
4_ A(2,4) B(3,6) C(0,y) noktaları veriliyor.IıACı-ıBCIı İFADESİNİN EN BÜYÜK OLMASI İÇİN y DEGERİ? (0)
5_ A(1.2) B(a,3) C(4,5) noktaları veriliyor.ıABı+ıBCIı İFADESİNİN EN KÜÇÜK OLMASI İÇİN A DEGERİ? (2)
6_A(5,1) B(2,3) C(1,y) noktaları veriliyor.ıACı+ıBCI İFADESİNİN EN küçük OLMASI İÇİN y DEGERİ? (13/5)