sin(α+β) = sinα.cosβ + cosα.sinβ
sin(α−β) = sinα.cosβ − cosα.sinβ
cos(α+β) = cosα.cosβ − sinα.sinβ
cos(α−β) = cosα.cosβ + sinα.sinβ
Formüllerin İspatları
Iki yayın toplam yada farkının trigonometrik oranları (toplam fark formülleri),Dönüşüm ve ters dönüşüm formülleri ve Yarım Açı Formüllerinin ispatlarını buradan indirebilirsiniz.İndirme sayfasına gittikten sonra Sarı klasöre tıklayarak indiriniz.
sin(α−β) = sinα.cosβ − cosα.sinβ
cos(α+β) = cosα.cosβ − sinα.sinβ
cos(α−β) = cosα.cosβ + sinα.sinβ
tan(α+β) =
tan α + tan β
1 − tan α.tan β
tan(α−β) =
tan α − tan β
1 + tan α.tan β
cot(α+β) =
cotα.cot β − 1
cotα + cotβ
cot(α−β) =
cotα.cot β + 1
cotα − cotβ
Formüllerin İspatları
Iki yayın toplam yada farkının trigonometrik oranları (toplam fark formülleri),Dönüşüm ve ters dönüşüm formülleri ve Yarım Açı Formüllerinin ispatlarını buradan indirebilirsiniz.İndirme sayfasına gittikten sonra Sarı klasöre tıklayarak indiriniz.
Teorem1.2. ve 1.4.
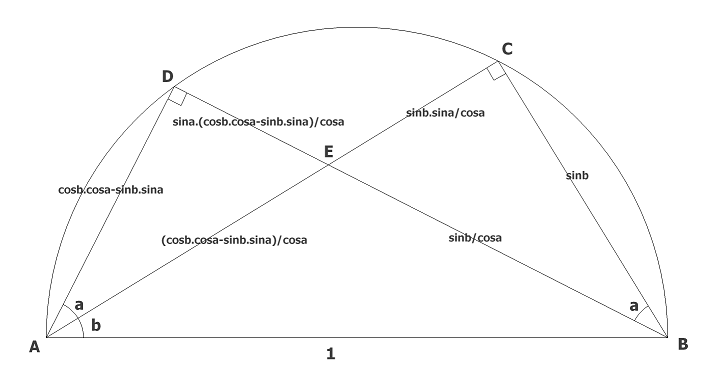
birim çemberi düşünelim

şekildeki gibi ADB ve ACB dik üçgenleri çizildiğinde
|AC|=cosb ve |CB|=sinb
|AD|=cos(a+b) ve |DB|=sin(a+b) olur
ECB dik üçgeninde sinüs ve cosinüsün tanımı gereği
|EC|=sinb.sina/cosa ve |EB|=sinb/cosa olur
|AC|=|AE|+|EC| oluğundan |AE|=cosb−(sinb.sina/cosa)=(cosb.cosa−sinb.sina)/cosa olur.
|AE| yi hipotenüs kabuleden ADE dik üçgeninde sinüs ve cosinüsün tanımından
|AD|=cosb.cosa−sinb.sina olur. Teorem1.2. ispatlanmış oldu.
|DE|=sina.(cosb.cosa−sinb.sina)/cosa
|DB|=|DE|+|EB| olduğundan
|DB|=sina.(cosb.cosa−sinb.sina)/cosa+sinb/cosa=sina.cosb−sinb.(sin²a/cosa)+sinb/cosa
=sina.cosb-sinb(sin²a−1)/cosa=sina.cosb-sinb(-cosa)=sina.cosb+sinb.cosa , Teorem1.4. ispatlanmış oldu.
birim çemberi düşünelim
şekildeki gibi ADB ve ACB dik üçgenleri çizildiğinde
|AC|=cosb ve |CB|=sinb
|AD|=cos(a+b) ve |DB|=sin(a+b) olur
ECB dik üçgeninde sinüs ve cosinüsün tanımı gereği
|EC|=sinb.sina/cosa ve |EB|=sinb/cosa olur
|AC|=|AE|+|EC| oluğundan |AE|=cosb−(sinb.sina/cosa)=(cosb.cosa−sinb.sina)/cosa olur.
|AE| yi hipotenüs kabuleden ADE dik üçgeninde sinüs ve cosinüsün tanımından
|AD|=cosb.cosa−sinb.sina olur. Teorem1.2. ispatlanmış oldu.
|DE|=sina.(cosb.cosa−sinb.sina)/cosa
|DB|=|DE|+|EB| olduğundan
|DB|=sina.(cosb.cosa−sinb.sina)/cosa+sinb/cosa=sina.cosb−sinb.(sin²a/cosa)+sinb/cosa
=sina.cosb-sinb(sin²a−1)/cosa=sina.cosb-sinb(-cosa)=sina.cosb+sinb.cosa , Teorem1.4. ispatlanmış oldu.
Teorem1.1. ve Teorem1.3.
cosinüsün çift sinüsün de tek fonksiyon olmasından dolayı
cos(a+b) de b yerine -b alındığında
cos(a−b)=cosa.cos(−b)-sina.sin(−b)=cosa.cosb-sina.(−sinb)=cosa.cosb+sina.sinb olur
sin(a+b) de b yerine -b yazılırsa
sin(a−b)=sina.cos(−b)+cosa.sin(−b)=sina.cosb+cosa.(−sinb)=sina.cosb−cosa.sinb olur
cosinüsün çift sinüsün de tek fonksiyon olmasından dolayı
cos(a+b) de b yerine -b alındığında
cos(a−b)=cosa.cos(−b)-sina.sin(−b)=cosa.cosb-sina.(−sinb)=cosa.cosb+sina.sinb olur
sin(a+b) de b yerine -b yazılırsa
sin(a−b)=sina.cos(−b)+cosa.sin(−b)=sina.cosb+cosa.(−sinb)=sina.cosb−cosa.sinb olur
ÖRNEK:
0<α<pi/2 olmak üzere,
ÇÖZÜM:

|CD|=9 olur.
ABC üçgeninde pisagordan
a²+1²=9²
a=4√5 olur.
O halde
0<α<pi/2 olmak üzere,
cos2α=
1
9
olduğuna göre, tanα değeri kaçtır ?
ÇÖZÜM:
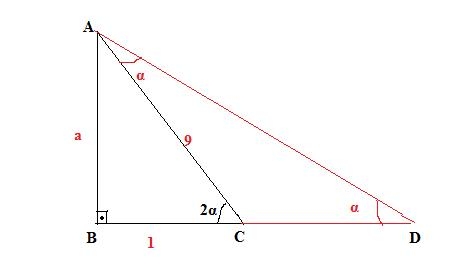
ABC üçgeninde cos2α=
1
9
uygulanırsa
|CD|=9 olur.
ABC üçgeninde pisagordan
a²+1²=9²
a=4√5 olur.
O halde
tanα=
|AB|
|BD|
=
4√5
10
=
2√5
5
bulunur.
Diğer çözümlü sorular alttadır.
