[Alp]

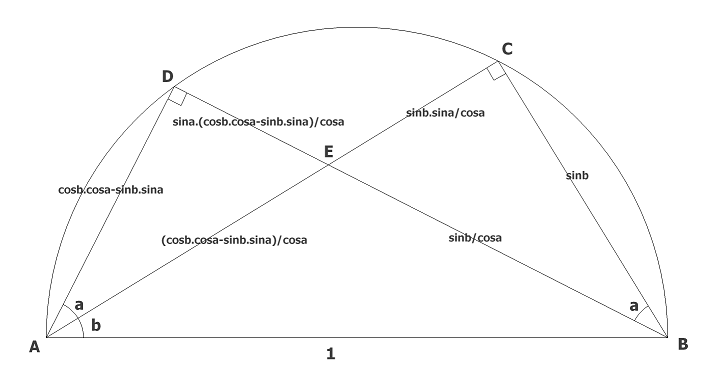
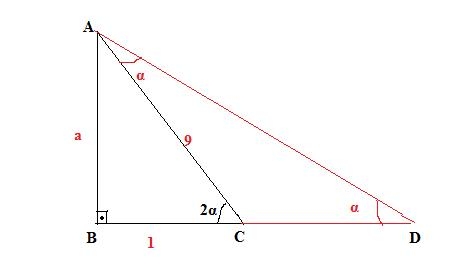
sin(α+β) = sinα.cosβ + cosα.sinβ

sin(α−β) = sinα.cosβ − cosα.sinβ


cos(α+β) = cosα.cosβ − sinα.sinβ

cos(α−β) = cosα.cosβ + sinα.sinβ

tan(α+β) =

tan α + tan β

1 − tan α.tan β

tan(α−β) =

tan α − tan β

1 + tan α.tan β

cot(α+β) =

cotα.cot β − 1

cotα + cotβ

cot(α−β) =

cotα.cot β + 1

cotα − cotβ

Formüllerin İspatları

Iki yayın toplam yada farkının trigonometrik oranları (toplam fark formülleri),Dönüşüm ve ters dönüşüm formülleri ve Yarım Açı Formüllerinin ispatlarını buradan indirebilirsiniz.İndirme sayfasına gittikten sonra Sarı klasöre tıklayarak indiriniz.

[gereksizyorumcu]

Teorem1.2. ve 1.4.


birim çemberi düşünelim



şekildeki gibi ADB ve ACB dik üçgenleri çizildiğinde
|AC|=cosb ve |CB|=sinb
|AD|=cos(a+b) ve |DB|=sin(a+b) olur

ECB dik üçgeninde sinüs ve cosinüsün tanımı gereği
|EC|=sinb.sina/cosa ve |EB|=sinb/cosa olur
|AC|=|AE|+|EC| oluğundan |AE|=cosb−(sinb.sina/cosa)=(cosb.cosa−sinb.sina)/cosa olur.

|AE| yi hipotenüs kabuleden ADE dik üçgeninde sinüs ve cosinüsün tanımından
|AD|=cosb.cosa−sinb.sina olur. Teorem1.2. ispatlanmış oldu.
|DE|=sina.(cosb.cosa−sinb.sina)/cosa

|DB|=|DE|+|EB| olduğundan
|DB|=sina.(cosb.cosa−sinb.sina)/cosa+sinb/cosa=sina.cosb−sinb.(sin²a/cosa)+sinb/cosa
=sina.cosb-sinb(sin²a−1)/cosa=sina.cosb-sinb(-cosa)=sina.cosb+sinb.cosa , Teorem1.4. ispatlanmış oldu.

[gereksizyorumcu]

Teorem1.1. ve Teorem1.3.

cosinüsün çift sinüsün de tek fonksiyon olmasından dolayı
cos(a+b) de b yerine -b alındığında
cos(a−b)=cosa.cos(−b)-sina.sin(−b)=cosa.cosb-sina.(−sinb)=cosa.cosb+sina.sinb olur

sin(a+b) de b yerine -b yazılırsa
sin(a−b)=sina.cos(−b)+cosa.sin(−b)=sina.cosb+cosa.(−sinb)=sina.cosb−cosa.sinb olur

[duygu95]

ÖRNEK:

0<α<pi/2 olmak üzere,

cos2α=

1

9

olduğuna göre, tanα değeri kaçtır ?

ÇÖZÜM:

ABC üçgeninde cos2α=

1

9

uygulanırsa

|CD|=9 olur.

ABC üçgeninde pisagordan

a²+1²=9²

a=4√5 olur.

O halde

tanα=

|AB|

|BD|

=

4√5

10

=

2√5

5

bulunur.