a ∈ R ve n ∈ Z (n ≥ 2) olmak üzere, n. kuvveti alındığında a'yı veren x reel sayılarına, a'nın n. kuvvette kökü denir
1) n çift iken
2) n tek iken dır.
dır.
1) n çift iken

2) n tek iken
 dır.
dır.Kök İçinde Köklü İfadeler

1)


2)


3)

4)
 (kök içerisinde n tane ifade vardır)
(kök içerisinde n tane ifade vardır)5)

6)

(a sayısı ardışık iki tamsayının çarpımına eşit ise sonuç büyük olan sayıya eşittir.)
7)

Köklü sayılar konu anlatımı ve soru çözümleri videolarını izlemek için tıklayınız.
Köklü Sayılarda Dört İşlem - Toplama Çıkarma Çarpma Bölme
1)

2)
 ;
;
3)

Köklü Sayılarda Eşlenik - Paydayı Rasyonel Yapma
1)

2)

3)
 ve
ve 
gibi ifadelerde payda eşleniği ile çarpılır.
ÖRNEK: 1

işleminin sonucu kaçtır ?
ÇÖZÜM 1:
Hepsini inceleyelim.
∛(−4)³=−4 olarak çıkar
√(-4)²=√16=4 olur.
∛4³=4
∜16=∜2⁴=2 olur. Bulduğumuz ifadeleri yerine yazalım.
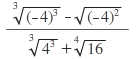
işleminin sonucu kaçtır ?
ÇÖZÜM 1:
Hepsini inceleyelim.
∛(−4)³=−4 olarak çıkar
√(-4)²=√16=4 olur.
∛4³=4
∜16=∜2⁴=2 olur. Bulduğumuz ifadeleri yerine yazalım.
-4-4
4+2
=-
8
6
=-
4
3
ÖRNEK 2:
M ve x birer gerçel sayıdır.
M=√x-2+x+1
olduğuna göre, M en az kaçtır ?
ÇÖZÜM 2:
M ifadesinin tanımlı olabilmesi için.
(x-2)≥0 olmalıdır.
x≥2 ise x'in alabileceği en küçük değere karşılık M ifadesi de en küçük değerini alır.
x=2 de en küçük değerini alır.
M=√2-2+2+1
min(M)=3 bulunur.
M ve x birer gerçel sayıdır.
M=√x-2+x+1
olduğuna göre, M en az kaçtır ?
ÇÖZÜM 2:
M ifadesinin tanımlı olabilmesi için.
(x-2)≥0 olmalıdır.
x≥2 ise x'in alabileceği en küçük değere karşılık M ifadesi de en küçük değerini alır.
x=2 de en küçük değerini alır.
M=√2-2+2+1
min(M)=3 bulunur.
ÖRNEK 3:

ÇÖZÜM 3:
Yerine yazarsak:



ifadeyi eşlenikle çarparsak

a
2
=
b
3
=k
olduğuna göre,
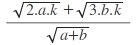
ifadesinin değeri kaçtır ?
ÇÖZÜM 3:
a
2
=
b
3
=k
a
2
=k ise a=2k olur.
b
3
=k ise b=3k olur.
Yerine yazarsak:
=
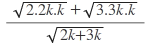
=
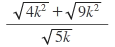
=
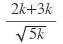
ifadeyi eşlenikle çarparsak
=
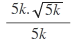
=√5k
ÖRNEK 4:
√6+√35-√6-√35
ifadesinin değeri nedir ?
ÇÖZÜM 4:
ifadelerin her birini √2 çarpıp bölelim.

Burada şu formulu kullanacağız. √x+2√a
a=a.1 ise
x=a+1 olmak üzere √x+2√a=√a+√1 olur.

ifadeyi eşlenikle çarparsak: √10 bulunur.
√6+√35-√6-√35
ifadesinin değeri nedir ?
ÇÖZÜM 4:
ifadelerin her birini √2 çarpıp bölelim.
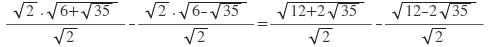
Burada şu formulu kullanacağız. √x+2√a
a=a.1 ise
x=a+1 olmak üzere √x+2√a=√a+√1 olur.
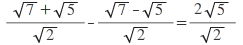
ifadeyi eşlenikle çarparsak: √10 bulunur.
ÖRNEK: 5
√20+√20+√...+√12-√12-√...
işleminin sonucu kaçtır ?
ÇÖZÜM 5:
Yukarıdaki formullerdeki 6. ve 7. formulleri bu soru için kullanacağız.
√20+√20+√... ifadesinde 20=4.5 olarak yazılabilir yani ardışık iki sayının çarpımıdır. Kök içindeki ifadeler toplam halinde olduğundan çarpanlardan büyük olanı yani 5'i alırız.
√12-√12-√... ifadesinde 12=3.4 olarak yazılabilir. 3 ve 4 ardışık sayılar olduğundan burada ise kök içindeki ifadelerin farkları olduğundan küçük olanı alırız. Yani 3'ü alırız.
√20+√20+√...+√12-√12-√...=5+3=8 olarak bulunur.
√20+√20+√...+√12-√12-√...
işleminin sonucu kaçtır ?
ÇÖZÜM 5:
Yukarıdaki formullerdeki 6. ve 7. formulleri bu soru için kullanacağız.
√20+√20+√... ifadesinde 20=4.5 olarak yazılabilir yani ardışık iki sayının çarpımıdır. Kök içindeki ifadeler toplam halinde olduğundan çarpanlardan büyük olanı yani 5'i alırız.
√12-√12-√... ifadesinde 12=3.4 olarak yazılabilir. 3 ve 4 ardışık sayılar olduğundan burada ise kök içindeki ifadelerin farkları olduğundan küçük olanı alırız. Yani 3'ü alırız.
√20+√20+√...+√12-√12-√...=5+3=8 olarak bulunur.
ÖRNEK 6:
∛4∛4∛4∛... + √27:√27:√27:√...
işleminin sonucu kaçtır ?
ÇÖZÜM 6:
Bu soru için yukarıdaki Kök içinde köklü ifadeler 4. ve 5. formulleri kullanacağız.
∛4∛4∛4∛...=3-1√4=2
√27:√27:√27:√...=2+1√27=3
∛4∛4∛4∛... + √27:√27:√27:√...=2+3=5 bulunur.
∛4∛4∛4∛... + √27:√27:√27:√...
işleminin sonucu kaçtır ?
ÇÖZÜM 6:
Bu soru için yukarıdaki Kök içinde köklü ifadeler 4. ve 5. formulleri kullanacağız.
∛4∛4∛4∛...=3-1√4=2
√27:√27:√27:√...=2+1√27=3
∛4∛4∛4∛... + √27:√27:√27:√...=2+3=5 bulunur.

Benzer konular
-
Mutlak Değer Nedir, Mutlak Değer Özellikleri Kuralları Formülleri
-
Üslü Sayılar Nedir? Üslü Sayıların Özellikleri, Üslü Sayı Kuralları Formülleri
-
Elipsin Analitik İncelenmesi Kuralları Özellikleri Formülü Formülleri
-
Çemberin Analitik İncelenmesi Kuralları Özellikleri Formülleri
-
Rasyonel Sayılarda Dört-4 İşlem Kuralları Özellikleri
