* M(a,b) çemberin merkezi ve r de çemberin yarıçapı olma üzere (x-a)²+(y-b)²= r²
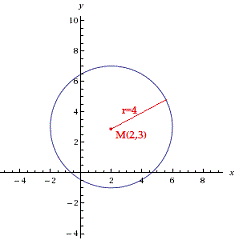
Örneğin; M(2,3) ve yarıçapı r=4 birim olan çember denklemi (x-2)²+(y-3)²= 4²
* Merkezi sıfır olan ve yarıçarpı r olan çember denklemi x²+y²= r² dir.
* Genel çember denklemi (x-a)²+(y-b)²= r² açılımından gelen
x² + y² + D.x + E.y + F = 0 dir.
* x² + y² + D.x + E.y + F = 0 genel denklemi ile verilen çemberin merkez koodinatları
M(a,b) ise a=-D/2 ve b= -E/2 dir ve yarıçap r= (1/2). √(D²+E²-4F)
*D²+E²-4F > 0 ise gerçel çember
D²+E²-4F =0 ise nokta çember
D²+E²-4F < 0 ise sanal çemberdir
* (x1,y1) noktasının x² + y² + D.x + E.y + F = 0 çemberine göre kuvveti p=x1² + y1² + D.x1 + E.y1 + F ve bu noktadan çembere çizilen teğetin uzunluğu t=√p dir.
* x²+y²= r² çemberi üzerindeki (x1,y1) noktasından çizilen teğetin denklemi x.x1+y.y1= r²
* (x-a)²+(y-b)²= r² çemberi üzerindki (x1,y1) noktsından çizilen teğetin denklemi (x1-a)(x-a)+(y1-b)(y-b)= r²
* x² + y² + D.x + E.y + F = 0 çemberi üzerindeki (x1,y1) noktasından çizilen teğetin denklemi
x.x1 + y.y1+ (D/2).(x+x1 ) + (E/2).(y+y1) + F = 0 . (x1,y1) noktası çember dışında ise bulunan denklemler değme kirişinin denklemidir.
Konu ile ilgili pdf dökümanını buradan indirebilirsiniz.İndirmek için Dosya>Orjinalini İndire tıklayınız.
Diğer indirme linki . İndirmek için Sağ tarafta "Karşıdan Yükle" linkine tıklayınız
Video anlatımı izlemek için buradaki sayfamıza bakınız