f(x)=a.sinx+b.cosx ifadesini "a" parantezine alalım.
f(x)=a(sinx+ba.cosx)
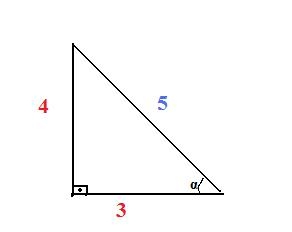
Bir dik üçgende b ve a dik kenar uzunlukları olarak aldığımızda b açısının karşısındaki açıya "y" dersek
tany=badersek
sinycosy=ba
f(x)=a(sinx+sinycosy.cosx)
f(x)=a.(sinx.cosy+siny.cosx)cosy=a.sin(x+y)cosy
Bu y açısı bulunan dik üçgende cosy yi bulmak istersek
cosy=a√a²+b²olacaktır.
O zaman şimdi bu f(x) eşitliğimiz
f(x)=a.sin(x+y)a/√a²+b²
f(x)= sin(x+y).√a²+b² yani
f(x)=a.sinx+b.cosx=sin(x+y).√a²+b² dır.
Herhangi bir açının sinüsü −1 ile 1 arasında olacağından ( −1≤ sin(x+y) ≤ 1 ) bu fonksiyonun en büyük veya en küçük değeri için sin(x+y) en büyük 1 veya en küçük −1 alınmalıdır.
O halde f(x)'in en büyük değeri
f(x)max=√a²+b²
f(x)'in en küçük değeri
f(x)min= − √a²+b²
Kaynak: http://goo.gl/CJas7