1) (111111)a/(a6-1) =1/7
esitligini saglayan a sayisi kaca esittir?(8)
2) (3213231)4 sayisinin on tabanindaki degerinin 16 ile bolumunden kalan kactir?(13)
3)A= 126!-1 sayisi veriliyor.
A sayisi 8 tabaninda yazilirsa sondan kac basamagindaki rakam 7 olur?(40)
4) Rakamlari farkli olmak uzere 12 tabaninda yazilabilecek en buyuk uc basamakli sayinin 10 tabanindaki degeri nedir?(1713)
5) x bir dogal sayi olmak uzere 27x -1 sayisinin 9 tabanindaki yazilisinda rakamlar toplami 192 olduguna gore x kactir? (16)
esitligini saglayan a sayisi kaca esittir?(8)
2) (3213231)4 sayisinin on tabanindaki degerinin 16 ile bolumunden kalan kactir?(13)
3)A= 126!-1 sayisi veriliyor.
A sayisi 8 tabaninda yazilirsa sondan kac basamagindaki rakam 7 olur?(40)
4) Rakamlari farkli olmak uzere 12 tabaninda yazilabilecek en buyuk uc basamakli sayinin 10 tabanindaki degeri nedir?(1713)
5) x bir dogal sayi olmak uzere 27x -1 sayisinin 9 tabanindaki yazilisinda rakamlar toplami 192 olduguna gore x kactir? (16)
1. Soru:
(111111)a ifadesini çözümlersek
1+a+a2+a3+a4+a5 gelir.
Bu ifadeyi (a6-1)'e bölüp 1/7 değerini bulmuş. Burda a6-1 ifadesinin açılımı (a-1)(1+a+a2+a3+a4+a5) şeklindedir. Sadeleştirmeler yapılırsa,
1/(a-1)=1/7
a-1=7 ve a=8 olur.
(111111)a ifadesini çözümlersek
1+a+a2+a3+a4+a5 gelir.
Bu ifadeyi (a6-1)'e bölüp 1/7 değerini bulmuş. Burda a6-1 ifadesinin açılımı (a-1)(1+a+a2+a3+a4+a5) şeklindedir. Sadeleştirmeler yapılırsa,
1/(a-1)=1/7
a-1=7 ve a=8 olur.
2. Soru:
(3213231)4 ifadesini çözümlersek
1+3.4+2.42+3.43+... şeklinde bir ifade gelecektir. 42'nden itibaren her çarpanda 16 bulunacağı için onların 16 ile bölümünden kalan 0 olacaktır. Geriye kalanlar ise 12+1=13 kalanı verecektir.
(3213231)4 ifadesini çözümlersek
1+3.4+2.42+3.43+... şeklinde bir ifade gelecektir. 42'nden itibaren her çarpanda 16 bulunacağı için onların 16 ile bölümünden kalan 0 olacaktır. Geriye kalanlar ise 12+1=13 kalanı verecektir.
4.soru
12 tabanında gelebilecek sayılar{0,1,2,3,4,5,6,7,8,9,10,11}'dir. yani 12 tabanının rakamları bunlardır.
3 basamaklı en büyük sayı(11109)12'dir. 10 tabanına çevirin.
11.12²+10.12+9=1584+120+9=1713
10-11 sayıları 12 tabanında birer rakamdır.
12 tabanında gelebilecek sayılar{0,1,2,3,4,5,6,7,8,9,10,11}'dir. yani 12 tabanının rakamları bunlardır.
3 basamaklı en büyük sayı(11109)12'dir. 10 tabanına çevirin.
11.12²+10.12+9=1584+120+9=1713
10-11 sayıları 12 tabanında birer rakamdır.
3. Soru:
10 tabanında bir sayı için 10'un asal çarpanlarından en büyük olanına yani 5'e bölüyorduk.
8 için de 8'in tek asal çarpanı olan 2'ye böleriz.
Zincirleme bölme yaparsak 120 gelir. 8=23 olduğundan 120/3=40 olur cevap.
10 tabanında bir sayı için 10'un asal çarpanlarından en büyük olanına yani 5'e bölüyorduk.
8 için de 8'in tek asal çarpanı olan 2'ye böleriz.
Zincirleme bölme yaparsak 120 gelir. 8=23 olduğundan 120/3=40 olur cevap.
5. Soru:
27x sayısının 9 tabanında, sonundaki 0 sayısını bilmediğimiz için şu şekilde yazarız
(.....0000000) bu sayıdan 1 çıkartınca rakamlar toplamı 192 oluyormuş.
a tane 8 olsun a.8=192 demek ki 24 tane 8 varmış. Burdan sonrası biraz karışık olacak nasıl anlatacağımı bilemedim (32)3x/2 bu ifadede 3x/2=24 müş demek ki, x=16 gelir ordan da.
27x sayısının 9 tabanında, sonundaki 0 sayısını bilmediğimiz için şu şekilde yazarız
(.....0000000) bu sayıdan 1 çıkartınca rakamlar toplamı 192 oluyormuş.
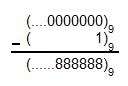
a tane 8 olsun a.8=192 demek ki 24 tane 8 varmış. Burdan sonrası biraz karışık olacak nasıl anlatacağımı bilemedim (32)3x/2 bu ifadede 3x/2=24 müş demek ki, x=16 gelir ordan da.
Diğer çözümlü sorular alttadır.
Sayı Sistemleri Çözümlü Sorular Taban Aritmetiği Çözümlü Sorular Taban Aritmetiği ile İlgili Sorular
Tüm Etiketler
Tüm Etiketler