1)x²+(2+m)x+m+14=0 denkleminin kökler toplamının, kökler çarpımının karekökü olabilmesi için m nin alabileceği değerler toplamı kaçtır?
2) x³-(m-2)x²+4x-m=0 denkleminin kökleri hem aritmetik hem geometrik dizi oluşturuyorsa m reel sayısının alabileceği değerler çarpımı kaçtır?
3) (4x²-4xy+3y²)/y²=4 eşitliğini sağlayan y nin x türünden değerleri toplamı nedir?
4) P(x+7) polinomunun P(x-8) ile bölümünden kalan 4x-a , P(x-8) polinomunun P(x+7) ile bölümünden kalan bx-12 olduğuna göre a+b=?
5) x4n-5.x2n+1+4x-6 polinomunun x³-x ile bölümünden kalan R(x) ise , R(x) polinomunun x-3 ile bölümünden kalan kaçtır?
6) P(ax)=x⁴+ax+b
P(bx)=x⁴+bx+a
P(a)=5 ise P(-2)=?
2) x³-(m-2)x²+4x-m=0 denkleminin kökleri hem aritmetik hem geometrik dizi oluşturuyorsa m reel sayısının alabileceği değerler çarpımı kaçtır?
3) (4x²-4xy+3y²)/y²=4 eşitliğini sağlayan y nin x türünden değerleri toplamı nedir?
4) P(x+7) polinomunun P(x-8) ile bölümünden kalan 4x-a , P(x-8) polinomunun P(x+7) ile bölümünden kalan bx-12 olduğuna göre a+b=?
5) x4n-5.x2n+1+4x-6 polinomunun x³-x ile bölümünden kalan R(x) ise , R(x) polinomunun x-3 ile bölümünden kalan kaçtır?
6) P(ax)=x⁴+ax+b
P(bx)=x⁴+bx+a
P(a)=5 ise P(-2)=?
ilk soruda kökler toplamının karesi kökler çarpımını verecek.
(-2-m)² = m+14
4+4m+m²=m+14
m²+3m-10=0
(x+5)(x-2)=5
2-5 = -3
(-2-m)² = m+14
4+4m+m²=m+14
m²+3m-10=0
(x+5)(x-2)=5
2-5 = -3
ilk soruda kökler toplamının karesi kökler çarpımını verecek.
(-2-m)² = m+14
4+4m+m²=m+14
m²+3m-10=0
(x+5)(x-2)=5
2-5 = -3
(-2-m)² = m+14
4+4m+m²=m+14
m²+3m-10=0
(x+5)(x-2)=5
2-5 = -3
yok mu çözen
cevap şıklarını yazman karşılığında neden olmasın. 
6)
P(ax)=x⁴+ax+b
P(bx)=x⁴+bx+a
a=b
P(a)=P(a.1)=1+a.1+b=5
a+b=4
a=b=2
P(-2)=P(2.-1)=1-2-2=-3
P(ax)=x⁴+ax+b
P(bx)=x⁴+bx+a
a=b
P(a)=P(a.1)=1+a.1+b=5
a+b=4
a=b=2
P(-2)=P(2.-1)=1-2-2=-3
S-2
Hem aritmetik hem de geometrik dizi oluşturuyorsa
x₁=x₂=x₃tür.
Buna göre yapabilirsiniz.
C.3
(4x²-4xy+3y²)=4y²
4x²-4xy-y²=0
Burada
Sınavda wolfram olmayacak diyebilirsin. O zaman sende wolframdan ilhamını alıp çözümünü yaparsın.
C.4
P(x+7) ve P(x-8) polinomların dereceleri eşittir.
Ve min. İkinci derecen bir polinomdur.
İşimiz kolay olsun. P(x)=cx²+dx+e olsun.
P(x+7)=cx²+(14c+d)x+49c+e
P(x-8)=cx²+(d-16c)x+64c+e
P(x+7)=P(x-8).B(x)+(4x-a)

P(x-8)=P(x+7).Q(x)+bx-12

a+b=-2
İşlem hatası yapmışımdır muhtemelen. Sorunun gidiş mantığını anladıysan eğer hatayı kendin düzeltebilirsin.
C.5
x4n-5.x2n+1+4x-6
R(x) 2. dereceden 1. dereceden olabilir. Veya sabit bir sayıdır.
R(x)=ax²+bx+c
x(x²-1)=0
x=0 x=1 x=-1
x=0 için;
c=-6
x=1 için;
a+b+c=-6
Bu durumda a+b=0
x=-1 için a-b+c=-4
a-b=2
a+b=0
a=1
b=-1
c=-6
R(x)=ax²+bx+c=x²-x-6
R(x)'in (x-3) ile bölümünden kalan x=3 için
9-3-6=0 dır.
***Verdiğim cevaplar biraz uzun gibi görünüyor. Ancak aklıma gelenler bunlar. Belki daha kısa cevaplar verenler olabilir.
Hem aritmetik hem de geometrik dizi oluşturuyorsa
x₁=x₂=x₃tür.
Buna göre yapabilirsiniz.
C.3
(4x²-4xy+3y²)=4y²
4x²-4xy-y²=0
Burada
Sınavda wolfram olmayacak diyebilirsin. O zaman sende wolframdan ilhamını alıp çözümünü yaparsın.
C.4
P(x+7) ve P(x-8) polinomların dereceleri eşittir.
Ve min. İkinci derecen bir polinomdur.
İşimiz kolay olsun. P(x)=cx²+dx+e olsun.
P(x+7)=cx²+(14c+d)x+49c+e
P(x-8)=cx²+(d-16c)x+64c+e
P(x+7)=P(x-8).B(x)+(4x-a)
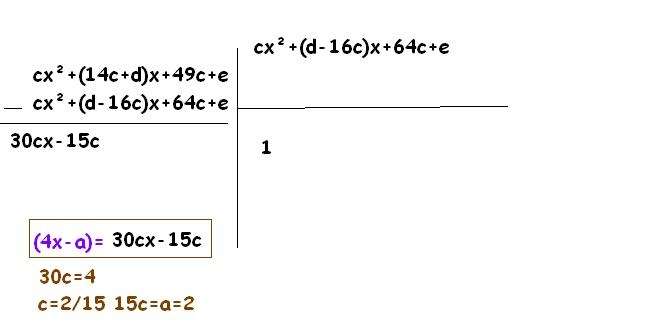
P(x-8)=P(x+7).Q(x)+bx-12

a+b=-2
İşlem hatası yapmışımdır muhtemelen. Sorunun gidiş mantığını anladıysan eğer hatayı kendin düzeltebilirsin.
C.5
x4n-5.x2n+1+4x-6
R(x) 2. dereceden 1. dereceden olabilir. Veya sabit bir sayıdır.
R(x)=ax²+bx+c
x(x²-1)=0
x=0 x=1 x=-1
x=0 için;
c=-6
x=1 için;
a+b+c=-6
Bu durumda a+b=0
x=-1 için a-b+c=-4
a-b=2
a+b=0
a=1
b=-1
c=-6
R(x)=ax²+bx+c=x²-x-6
R(x)'in (x-3) ile bölümünden kalan x=3 için
9-3-6=0 dır.
***Verdiğim cevaplar biraz uzun gibi görünüyor. Ancak aklıma gelenler bunlar. Belki daha kısa cevaplar verenler olabilir.
C.3
(4x²-4xy+3y²)=4y²
4x²-4xy-y²=0
Burada
Sınavda wolfram olmayacak diyebilirsin. O zaman sende wolframdan ilhamını alıp çözümünü yaparsın.
(4x²-4xy+3y²)=4y²
4x²-4xy-y²=0
Burada
Sınavda wolfram olmayacak diyebilirsin. O zaman sende wolframdan ilhamını alıp çözümünü yaparsın.
O zaman işlemi kendin yaparsın frk bundan basit ne var.
