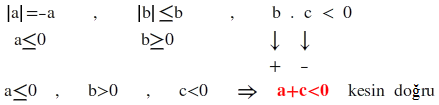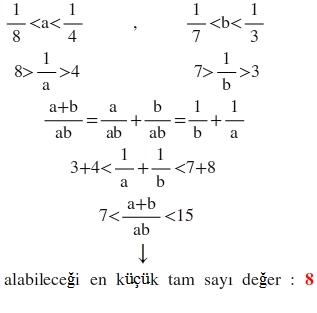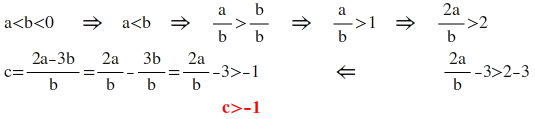1) -a<-b<0 √(a-b)2 + ∛(2a+b)3=15 eşitliğinde b nin alabileceği en büyük tamsayı değeri kaçtır?
cevap:4
2)|a|= -a |b|≤b b.c<0 olduğuna göre aşağıdakilerden hangisi kesinlikle doğrudur?
a) a>b b)b< c c)a<c d)a+b<0 E) a+c< 0
3)-7/2 <1/x-2< -1/3 eşitsilik sistemini sağlayan kaç farklı x tamsayısı vardır?
cevap: 2
4)1/8< a < 1/4 1/7 < b < 1/3 olduğuna göre a+b/a.b ifadesinin alabileceği en küçük tamsayı değeri kaçtır? cevap:8
5) a< b< 0 c= 2a-3b/ b olduğuna göre c nin en geniş çözüm kümesi ? cevap:c > -1