SORU 1:
ÇÖZÜM 1:
öncelikle eştsizliği ayrı ayrı sıfır yapan değerlere bakalım;
pay için; 2x-5=0 ise x=5/2
payda için ; x+4=0 ise x=-2
Bunları tabloda gösterelim;

Tabloya bakarsa bizim aradığımız bölgenin (-4,5/2] aralığı olduğunu görürüz. Bu durumda
çözüm kümemiz Ç.K=(-4,5/2] bulunur.
------------------------------------------------------------------------
SORU 2:
ÇÖZÜM 2:
Bu çarpanın baş katsayısı -2 yani negatiftir.
Bu üç çarpandan sadece birinin baş katsayısı eksi olduğundan son bölgenin (en sağ bölgenin) işareti eksidir. Diğer bölgelerin işaretleri sağdan sola doğru değiştirilerek bulunur.

Tabloya göre;
Buna göre,
(Not: +&= artı sonsuzu ifade eder )
-----------------------------------------------------------------------------
SORU 3:
ÇÖZÜM 3:
5x-7=0 =>x=7/5
x-2=0 =>x=2 (paydayı sıfır yapar)
x+1=0=>x=-1(paydayı sıfır yapar)

Tabloya bakarsak işareti negatif olan bölgeleri arıyoruz Bu durumda ;
------------------------------------------------------------------------------------------------------------
SORU 4:
x²+3x-4≤0
x²-5x+6>0
eşitsizliğinin çözüm kümesi nedir ?
ÇÖZÜM 4:
x²+3x-4=(x+4).(x-1)=0 olduğundan x=-4,1
x²-5x+6=(x-2).(x-3)=0 olduğundan x=2,3

Tabloya göre;
biz birinci eşitsizlikte sıfırdan büyük olanı (+ ile taradığım), ikinci eşitsizlikte sıfırdan küçük olanı(- ile taradığım) arıyoruz.
Tabloda istediğimiz kısımların kesişimi bize sistemin çözüm kümesini verir.
Ç.K=[-4,-1] bulunur. (1 ve 4 dahildir çünkü bu iki sayı da 1. eşitsizliğin kökleri 1. eşitsizlikte küçük eşit olduğundan dahildir.)
---------------------------------------------------------------------------
SORU 5:
x²-4<0
x²-2x-3≥0
eşitsizlik sisteminin çözüm kümesini bulunuz.
ÇÖZÜM 5:
x²-4=0 => x=2,-2
x²-2x-3=0 =>x=3,-1

Tabloya göre;
Birinci eşitsizlikte bize sıfırdan küçük olan kısım(- olarak taradığım) lazım, ikinci eşitsizlikte ise bize sıfırdan büyük(+ olarak taradığım) ve eşit olan kısım lazım. Bu tabloda bu ikisinin kesişimi sistemin çözüm kümesini oluşturur.
Ç.K=(-2,-1] bulunur. (Burada 1'i dahil olarak almamın sebebi eşitsizliğinin büyük eşit olmasından kaynaklanıyor.)
--------------------------------------------------------------------------------------------------------
SORU 6:
|x+4|≤5 ifadesinin çözüm kümesi nedir ?
ÇÖZÜM:
1. yol
-5≤x+4≤5
-9≤x≤1
2.yol
|x+4|=5
x+4=5 veya x+4=-5
x=1 veya x=-9

Tabloya göre bizim aradığımız aralık -9 ve 1 arası ama eşitsizliğimizde eşitlik olduğundan
Ç.K=[-9,1] bulunur.
----------------------------------------------------------------------------------------------------------
SORU 7:
(x²-4).|x-1|≤0 ise çözüm kümesini bulunuz.
ÇÖZÜM 7:
x=2 ve x=-2 olur.

Bizim aradığımız aralık sıfırdan küçük olduğundan tabloda "-" ile taradığım kısıma bakarız aynı zamanda dahil olduğundan kapalı aralıkta gösteririz.
Ç.K=[-2,2] bulunur.
----------------------------------------------------------------------------------------------------------
SORU 8:
ÇÖZÜM 8:
ifadeyi sıfır yapan değerlere bakalım;
x=2,-2 ve çift katlı
x=-10,11
x=-3 çift katlı fakat dahil değil.

sıfırdan büyük aralıklara bakacağız (+ ile taradığım) ama mutlak değerli ifadeleri de dahil edeceğiz.
Ç.K=(-&,-10)∪[11,+&)∪{-2,2}
-------------------------------------------------------------------------------------------------
SORU 9:
ÇÖZÜM 9:
önce ifadeyi sıfır yapan değerlere bakalım
x=0 ve x=1/20
|x-1|-5=0
|x-1|=5
x-1=5 veya x-1=-5
x=6,x=-4

Tabloda sıfırdan büyük olan kısımları (+ olarak taradığım) arıyoruz.;
Ç.K=(-4,0)∪(1/20,6)
-------------------------------------------------------------------------------------------
SORU 10:
ÇÖZÜM 10:
sadece payda kök bulabiliriz. x-1=0 için x=-1 olur. Çünkü |x|+10=0 olamaz.
o halde eşitsizliğimizin tablosu;

şeklinde olur biz sıfırdan küçük olan kısmı(- ile taradığım) arıyoruz.
Ç.K=(-&,1] bulunur. (1 dahil çünkü eşitlik var.)
2x-5
x+4
≤0 eşitsizliğinin çözüm kümesi nedir ?
ÇÖZÜM 1:
öncelikle eştsizliği ayrı ayrı sıfır yapan değerlere bakalım;
pay için; 2x-5=0 ise x=5/2
payda için ; x+4=0 ise x=-2
Bunları tabloda gösterelim;
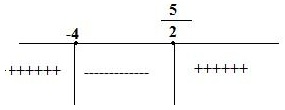
Tabloya bakarsa bizim aradığımız bölgenin (-4,5/2] aralığı olduğunu görürüz. Bu durumda
çözüm kümemiz Ç.K=(-4,5/2] bulunur.
------------------------------------------------------------------------
SORU 2:
(-2x+3).(x+2)
x-5
≤0 eşitsizliğinin çözüm kümesini bulunuz.
ÇÖZÜM 2:
-2x+3=0 => x=
3
2
Bu çarpanın baş katsayısı -2 yani negatiftir.
Bu üç çarpandan sadece birinin baş katsayısı eksi olduğundan son bölgenin (en sağ bölgenin) işareti eksidir. Diğer bölgelerin işaretleri sağdan sola doğru değiştirilerek bulunur.
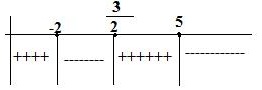
Tabloya göre;
-2≤x≤
3
2
veya x>5 olur.
Buna göre,
Ç=[-2,
3
2
]∪(5,+&)
(Not: +&= artı sonsuzu ifade eder )
-----------------------------------------------------------------------------
SORU 3:
x-1
x-2
≤
x-3
x+1
Eşitsizliğinin çözüm kümesini bulunuz.
ÇÖZÜM 3:
x-1
x-2
-
x-3
x+1
≤0
(x-1).(x+1)-(x-3).(x-2)
(x-2).(x+1)
≤0
(x²-1)-(x²-5x+6)
(x-2).(x+1)
≤0
5x-7
(x-2).(x+1)
≤0
5x-7=0 =>x=7/5
x-2=0 =>x=2 (paydayı sıfır yapar)
x+1=0=>x=-1(paydayı sıfır yapar)
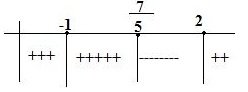
Tabloya bakarsak işareti negatif olan bölgeleri arıyoruz Bu durumda ;
Ç.K=(-&,-1)∪[
7
5
,2)
------------------------------------------------------------------------------------------------------------
SORU 4:
x²+3x-4≤0
x²-5x+6>0
eşitsizliğinin çözüm kümesi nedir ?
ÇÖZÜM 4:
x²+3x-4=(x+4).(x-1)=0 olduğundan x=-4,1
x²-5x+6=(x-2).(x-3)=0 olduğundan x=2,3
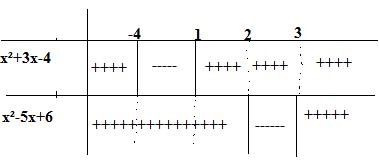
Tabloya göre;
biz birinci eşitsizlikte sıfırdan büyük olanı (+ ile taradığım), ikinci eşitsizlikte sıfırdan küçük olanı(- ile taradığım) arıyoruz.
Tabloda istediğimiz kısımların kesişimi bize sistemin çözüm kümesini verir.
Ç.K=[-4,-1] bulunur. (1 ve 4 dahildir çünkü bu iki sayı da 1. eşitsizliğin kökleri 1. eşitsizlikte küçük eşit olduğundan dahildir.)
---------------------------------------------------------------------------
SORU 5:
x²-4<0
x²-2x-3≥0
eşitsizlik sisteminin çözüm kümesini bulunuz.
ÇÖZÜM 5:
x²-4=0 => x=2,-2
x²-2x-3=0 =>x=3,-1
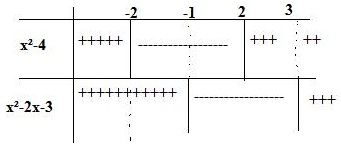
Tabloya göre;
Birinci eşitsizlikte bize sıfırdan küçük olan kısım(- olarak taradığım) lazım, ikinci eşitsizlikte ise bize sıfırdan büyük(+ olarak taradığım) ve eşit olan kısım lazım. Bu tabloda bu ikisinin kesişimi sistemin çözüm kümesini oluşturur.
Ç.K=(-2,-1] bulunur. (Burada 1'i dahil olarak almamın sebebi eşitsizliğinin büyük eşit olmasından kaynaklanıyor.)
--------------------------------------------------------------------------------------------------------
SORU 6:
|x+4|≤5 ifadesinin çözüm kümesi nedir ?
ÇÖZÜM:
1. yol
-5≤x+4≤5
-9≤x≤1
2.yol
|x+4|=5
x+4=5 veya x+4=-5
x=1 veya x=-9

Tabloya göre bizim aradığımız aralık -9 ve 1 arası ama eşitsizliğimizde eşitlik olduğundan
Ç.K=[-9,1] bulunur.
----------------------------------------------------------------------------------------------------------
SORU 7:
(x²-4).|x-1|≤0 ise çözüm kümesini bulunuz.
ÇÖZÜM 7:
x=2 ve x=-2 olur.
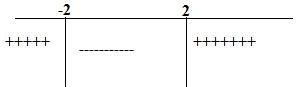
Bizim aradığımız aralık sıfırdan küçük olduğundan tabloda "-" ile taradığım kısıma bakarız aynı zamanda dahil olduğundan kapalı aralıkta gösteririz.
Ç.K=[-2,2] bulunur.
----------------------------------------------------------------------------------------------------------
SORU 8:
|x²-4|.(x²-x-110)
|x+3|
eşitsizliğinin çözüm kümesini bulunuz.
ÇÖZÜM 8:
ifadeyi sıfır yapan değerlere bakalım;
x=2,-2 ve çift katlı
x=-10,11
x=-3 çift katlı fakat dahil değil.
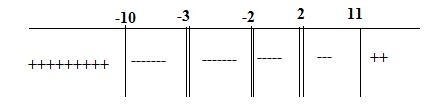
sıfırdan büyük aralıklara bakacağız (+ ile taradığım) ama mutlak değerli ifadeleri de dahil edeceğiz.
Ç.K=(-&,-10)∪[11,+&)∪{-2,2}
-------------------------------------------------------------------------------------------------
SORU 9:
x-20x²
|x-1|-5
>0 eşitsizliğinin çözüm kümesini bulunuz.
ÇÖZÜM 9:
önce ifadeyi sıfır yapan değerlere bakalım
x=0 ve x=1/20
|x-1|-5=0
|x-1|=5
x-1=5 veya x-1=-5
x=6,x=-4
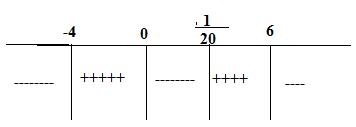
Tabloda sıfırdan büyük olan kısımları (+ olarak taradığım) arıyoruz.;
Ç.K=(-4,0)∪(1/20,6)
-------------------------------------------------------------------------------------------
SORU 10:
x-1
|x|+10
≤0 eşitsizliğinin çözüm kümesini bulunuz.
ÇÖZÜM 10:
sadece payda kök bulabiliriz. x-1=0 için x=-1 olur. Çünkü |x|+10=0 olamaz.
o halde eşitsizliğimizin tablosu;
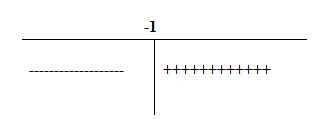
şeklinde olur biz sıfırdan küçük olan kısmı(- ile taradığım) arıyoruz.
Ç.K=(-&,1] bulunur. (1 dahil çünkü eşitlik var.)
eline sağlık duygu
Diğer çözümlü sorular alttadır.
Çözümlü Eşitsizlik Soruları Eşitsizlik Soruları ve Çözümleri Eşitsizliklerde Tablo Oluşturma Soruları Eşitsizliklerin Çözüm Kümesi Soruları
Tüm Etiketler
Tüm Etiketler
