1. f : R → R fonksiyonu,
İle tanımlansın, f fonksiyonunun x0 = 1 noktasında sürekli olup olmadığını bulunuz.
Çözüm:
limx→1⁻=limx→1⁻x²-1x-1=limx→1⁻(x-1)(x+1)x-1=limx→1⁻(x+1) = 2
limx→1⁺=limx→1⁺(-x²-2x+5) = -(1⁺)² - 2(1⁺) + 5 = -1 -2 +5 = 2
f(1) = 2
limx→1f(x) = 2 = f(1)
Olduğundan f(x) fonksiyonu x0 = 1 noktasında süreklidir.
2.f(x) =1x-2, x0 = 2 noktasında süreklimidir?
Çözüm:
limx→2⁺1x-2=10⁺= +∞
limx→0⁻1x-2=12⁻-0=10⁻= -∞
Limit yok x = 2 noktasında sürekli değildir.
3.ise f(x) nin R de sürekli olması için a ve b ne olmalıdır?
Çözüm:
limx→3⁻f(x) = 1,limx→3⁺f(x) = 3a+b,limx→5⁻f(x) = 5a+b,limx→5⁺f(x) = 7, f(3) = 1, f(5) = 7
limx→3⁺=limx→3⁺f(x) = f(3) ⇒ 3a + b
limx→5⁻f(x) = f(5) ⇒ 5a + b
5a + b = 7
3a + b = 1
_________
2a = 6
a = 3 ve b = -8
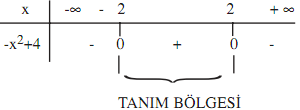
4. f(x) = √-x² + 4 fonksiyonların sürekli olduğu kümeyi belirleyiniz.
Çözüm:
Sürekli olduğu aralık;
-x² + 4 ≥ 0
-x² + 4 = 0
x² = 4
x1,2 = ±2
Sürekli olduğu aralık {x : -2 ≤ x ≤ 2, x ∈R }
5.
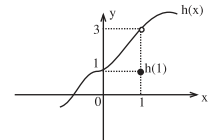
Şekildeki h fonksiyonu x = 1 noktasında sürekli midir?
Çözüm:
limx→1⁻h(x) = 3 =limx→1⁺h(x)
Ancak h(1) = 1 olduğu için h fonksiyonu x = 1 noktasında sürekli değildir.

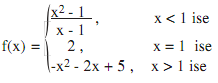
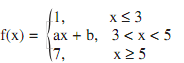 ise f(x) nin R de sürekli olması için a ve b ne olmalıdır?
ise f(x) nin R de sürekli olması için a ve b ne olmalıdır?