ELİPS
1)Bir atlet, elips şeklindeki bir pistte koşmaktadır. Atlet pistte koşarken elipsin merkezine en yakın olduğu mesafe 40 metre, en uzak olduğu mesafe 50 metre olduğuna göre, bu pistin odakları arasındaki uzaklık kaç metredir?
Çözüm:
2a=50 a=25
2b=40 b=20
a²=b²+c²
c=30 2c=60
Cevabımız 60.
2)Analitik düzlemde, odakları F(-4,0) ve F(4,0) olan elips P(0,3) noktasından geçtiğine göre, bu elipsin dış merkezliği kaçtır?
Çözüm:
Öncelikle dış merkezliği bilmeyenler için tanımını yazayım:
Elipsin odaklar arası uzaklığının, asal eksen uzunluğuna oranına elipsin dış merkezliği denir. e ile gösterilir.
e=2c/2a=c/a 0<e<1
a²=b²+c²
a²=9+16 a=5
e=c/a=4/5
Cevabımız 4/5.
3)Asal çemberinin denklemi x²+y²=25 ve yedek çemberinin denklemi x²+y²=15 olan elipsin odakları Ox ekseni üzerinde olduğuna göre, bu elipsin denklemi?
Çözüm:

x²/25+y²/15=1
3x²+5y²=75
Cevabımız 3x²+5y²=75.
4)Elipsin odak noktasından geçen en kısa kirişin uzunluğuna elipsin parametresi denir. Buna göre, x²/64+y²/36=1 olan elipsin parametresi kaçtır?
Çözüm:
2p=2b²/a
2p=2.36/8 2p=9
Cevabımız 9.
5)Dik koordinat düzleminde y=mx+2 doğrusunun x²/4+y²=1 elipsine teğet olabilmesi için m nin alabileceği pozitif değer kaçtır?
Çözüm:
Öncelikle elipsle herhangi bir doğrunun durumlarını inceleyelim:
x²/a²+y²/b²=1 ile y=mx+n doğrusunun ortak çözümü yapılırsa,
*Doğru elipse teğetse a².m²+b²-n²=0
**Doğru elipsi iki noktada kesiyorsa a².m²+b²-n²>0
***Doğru elipsi kesmiyorsa a².m²+b²-n²<0
(daha kısa bir yolu vardı yalnız aklıma gelmedi )
)
Buna göre;
a².m²+b²-n²=0
4.m²+14=0
4m²=3 m²=3/4 m=√3/4
Cevabımız √3/4.
6)y=x+n doğrusu x²/16+y²/9=1 elipsine teğet olduğuna göre, n=?
Çözüm:
16+9-n²=0 n=5
Cevabımız 5.
Bir iki tanede ek bilgi vereyim.
*x=a²/c veya x=-a²/c doğruları elipsin doğrultman denklemleridir.
*x=a.cosα y=b.sinα eşitlikleri elipsin parametrik denklemleridir.
cos²α=x²/a² sin²α=y²/b²
cos²α+sin²α=1 olduğundan x²/a²+y²/b²=1
* x²/a²+y²/b²=1 elipsi için
Alan= ∏.a.b
Çevre= ∏.(a+b)
1)Bir atlet, elips şeklindeki bir pistte koşmaktadır. Atlet pistte koşarken elipsin merkezine en yakın olduğu mesafe 40 metre, en uzak olduğu mesafe 50 metre olduğuna göre, bu pistin odakları arasındaki uzaklık kaç metredir?
Çözüm:
2a=50 a=25
2b=40 b=20
a²=b²+c²
c=30 2c=60
Cevabımız 60.
2)Analitik düzlemde, odakları F(-4,0) ve F(4,0) olan elips P(0,3) noktasından geçtiğine göre, bu elipsin dış merkezliği kaçtır?
Çözüm:
Öncelikle dış merkezliği bilmeyenler için tanımını yazayım:
Elipsin odaklar arası uzaklığının, asal eksen uzunluğuna oranına elipsin dış merkezliği denir. e ile gösterilir.
e=2c/2a=c/a 0<e<1
a²=b²+c²
a²=9+16 a=5
e=c/a=4/5
Cevabımız 4/5.
3)Asal çemberinin denklemi x²+y²=25 ve yedek çemberinin denklemi x²+y²=15 olan elipsin odakları Ox ekseni üzerinde olduğuna göre, bu elipsin denklemi?
Çözüm:
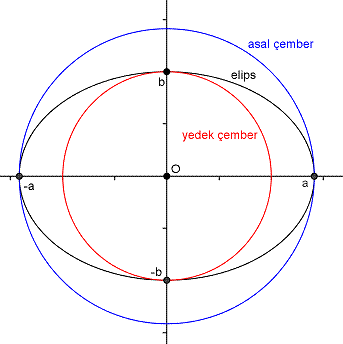
x²/25+y²/15=1
3x²+5y²=75
Cevabımız 3x²+5y²=75.
4)Elipsin odak noktasından geçen en kısa kirişin uzunluğuna elipsin parametresi denir. Buna göre, x²/64+y²/36=1 olan elipsin parametresi kaçtır?
Çözüm:
2p=2b²/a
2p=2.36/8 2p=9
Cevabımız 9.
5)Dik koordinat düzleminde y=mx+2 doğrusunun x²/4+y²=1 elipsine teğet olabilmesi için m nin alabileceği pozitif değer kaçtır?
Çözüm:
Öncelikle elipsle herhangi bir doğrunun durumlarını inceleyelim:
x²/a²+y²/b²=1 ile y=mx+n doğrusunun ortak çözümü yapılırsa,
*Doğru elipse teğetse a².m²+b²-n²=0
**Doğru elipsi iki noktada kesiyorsa a².m²+b²-n²>0
***Doğru elipsi kesmiyorsa a².m²+b²-n²<0
(daha kısa bir yolu vardı yalnız aklıma gelmedi
Buna göre;
a².m²+b²-n²=0
4.m²+14=0
4m²=3 m²=3/4 m=√3/4
Cevabımız √3/4.
6)y=x+n doğrusu x²/16+y²/9=1 elipsine teğet olduğuna göre, n=?
Çözüm:
16+9-n²=0 n=5
Cevabımız 5.
Bir iki tanede ek bilgi vereyim.
*x=a²/c veya x=-a²/c doğruları elipsin doğrultman denklemleridir.
*x=a.cosα y=b.sinα eşitlikleri elipsin parametrik denklemleridir.
cos²α=x²/a² sin²α=y²/b²
cos²α+sin²α=1 olduğundan x²/a²+y²/b²=1
* x²/a²+y²/b²=1 elipsi için
Alan= ∏.a.b
Çevre= ∏.(a+b)
Eline, aklına sağlık
Eline sağlık.
Eline, aklına sağlık
Eline sağlık.
