Fonksiyon sorularım

1) f: N+->R
f(x+1)=x.f(x)
f(1)=1 olduğuna göre f(100) nedir ?

cvp:99!

2) Gerçel sayılar kümesinde tanımlı aşağıdaki fonksiyonlardan hangileri bire bir dir?
a)F(x)=3x+5
b)f(x)= -2x+8
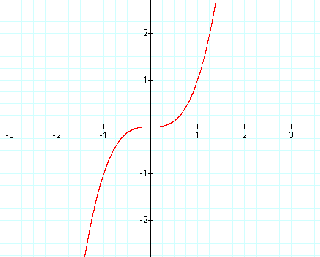
c)f(x)= x²
d)f(x)=x³

Bu tip sorularda doğrulama nasıl sağlanıyor bilmiyorum

cvp: ( a,b ve d)

3) A=(1,2,3,4)
B=(2,4,6,8)
olduğuna göre A dan Bye kaç tane bire bir ve örten fonksiyon tanımlanabilir?

cvp:24

4)f birim fonksiyon olmak üzere
f(x) = (a-5)+(b+1)x+c-2 olduğuna göre a+b+c toplamı kaçtır?

cvp:8

5)f birim fonksiyon olmak üzere
f(4x+1)=(a-2)x+3b-11 olduğuna göre a.b çarpımı kaçtır?

cvp:24

1)
f(2)=1f(1)
f(3)=2f(2)
.
.
.
f(100)=99f(99)
Taraf tarafa çarparsak
f(100)=99!

2) Bire bir olması için her bir y değerine yalnızca bir x değeri gitmelidir.
a,b ve d'de bu şart sağlanırken x²'de x'in mutlak değerce eşit iki değeri aynı görüntüye gitmektedir.
Ya da fonksiyonların grafiğine bakarsınız
a ve b bir doğru olduğu için bire birdir.
d
c ise paraboldür ve y eksenine göre simetriktir.

3)
A'daki her elemanın B'de yalnız bir elemana gitmesi gerekir.
İlk seçimde B'den 4 eleman, 2. seçimde 3 eleman, 3. seçimde 2 eleman, 4. seçimde kalan 1 eleman seçilebilir.
4.3.2.1=24

4) f(x) birim fonksiyon ise f(x)=x olmalıdır.

x=a-5+(b+1)x+c-2

b+1=1
b=0
a+c-7=0
a+c=7

a+b+c=7

5)
4x+1=(a-2)x+3b-11
a-2=4
a=6
3b-11=1
3b=12
b=4
a.b=6.4=24

Çok teşekkür ederim