(x-z).(x-y)<0
ise hangisi doğru olabilir?x<y<z y<x<z z<y<x x<z<y y<z<x
a,b,c reel sayılardır.
a.b.c<0
b<c
ise hangisi daima doğrudur? a.b<0 b.c<0 a.b<a.c b-a<c-a a-b-c>0
x>y ve x.z-z.y<0 ise hangisi daima doğrudur?
x>z z<0 x²>y² 2x+24>0 5x+3y<0
m,n,r pozitif tamsayılardır.
ise m+n+r toplamının en küçük değeri kaçtır? cevap 10
x ve y birer tamsayıdır.
-5<x≤3 ve -4<y≤2 ise (x³-y³) ifadesinin en büyük değeri kaçtır? cevap:54

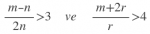 ise m+n+r toplamının en küçük değeri kaçtır? cevap 10
ise m+n+r toplamının en küçük değeri kaçtır? cevap 10
