[Yardım]

1- yarıçapları oranı 1/3 olan iki kürenin hacimleri oranı kaçtır?

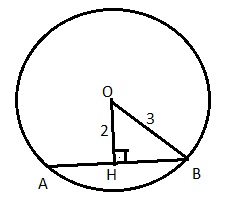
2- hacmi 36∏ cm³ olan bir küre, merkezine 2 cm uzaklıkta bir düzlemle kesiliyor. Meydana gelen ara kesit dairesinin alanını bulunuz.

3- taban yarıçapı 4 cm ve yüksekliği 6 cm olan bir silindirin yarısı su doludur. Silindirin içine yarıçapı 2 cm olan küre biçiminde bir cisim atıldığında suyun yüksekliği kaç cm olur ? ∏=3

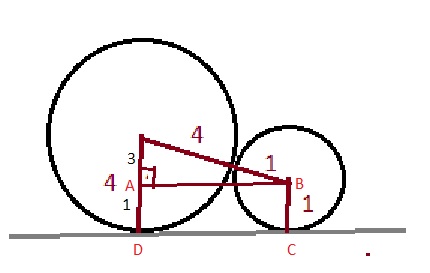
4- yarıçapları sırasıyla 4 cm ve 1 cm olan iki küre birbirlerine ve zemine teğettir. Buna göre kürelerin zemine değdiği noktalar arasındaki uzaklık kaç cm'dir?

5- birbirine eş koniler tepe noktalarından birleştirilerek küre elde ediliyor. Konilerden yararlanarak kürenin hacim bağıntısını oluşturunuz.

[korkmazserkan]

C-1) yarıçapları r ve 3r olsun

[Serkan A.]

C-2) ilk önce bu kürenin yarıçapını bulalım. hacim formülünden 4.pi.r³/3=36.pi den r=3 çıkar. Kürenin kesilmiş halini şekilde gibi 2 boyutlu olarak çizdim.



Kesilen yüzey [AB] boyunca kesilmiştir. [OH] dik [AB] olacaktır. Buradaki dik üçgenden |HB|=√5 çıkacaktır.

Bu [HB],[AB] boyunca kesilen daire kesitinin yarıçapı olacaktır. Ozaman bu kesitin alanı pi.(√5)²=5pi

[Serkan A.]

C-3) Silindir yarısına kadar dolu ise şu an 3 cm yüksekliktedir. Bu 3 cm nin üzerine kürenin yükselteceği su yüksekliği ile birlikteki uzunluğu orantı ile bulacağız.

Krüenin hacmi:4.3.2²/3=16cm³
Silindirin hacmi 3.4².6= 288 cm³
Yarım dolu silindirin hacmi: 144cm³

144cm³ iken 3 cm ise
144+16 iken kaç cmdir?
---------------------
D.O.

Birlikteki yükseklik=160.3/144= 3,3 cm dir.

[Serkan A.]

C-4)



istenen [CD] ile [AB] nin uzunlukları eşittir. [AB] yi biz çizdik.Diküçgenden |AB|=4 bulunur. Cevap 4 tür.

[Serkan A.]

C-5) konilerin birleşmesi ile kürenin nasıl olacağı alt taraftaki resimde mevcuttur.




Burada koni sayısı ne kadar çok artırırsak konilerin hacimlerinin toplamı kürenin hacmine o kadar yakın değer çıkar.

Uygun şekilde çizmek çok vakit alacağı için alttaki şekildeki piramitleri koni gibi düşünün.

a₁,a₂,a₃,...,a_n konilerin taban alanlarıdır. h, bir koninin yüksekliği olsun.



Çok sayıda koni olduğunu düşünelim. Buradaki konilerin hacimlerini toplayalım.

(h.a₁/3)+(h.a₂/3)+(h.a₃/3)+...+(h.a_n/3)=(h/3).(a₁+a₂+a₃+...+a_n)

Buradaki a₁+a₂+a₃+...+a_n toplam alanı, h uzunluğu kürenin r yarıçapına yaklaştıkça yani konileri çok sayıda küre içine yerleştirdiğimizde kürenin yüzey alanına eşit olacaktır.

a₁+a₂+a₃+...+a_n≅4.pi.r²

o zaman konilerin toplam hacmini bulurken ki a₁+a₂+a₃+...+a_n yerine çok yakın bir değer olacak 4.pi.r² yi yazarsak

= (h/3).(4.pi.r²)= 4.pi.h.r²/3 elde edilir.

h uzunluğu kürenin r yarıçapına yaklaştıkça yani konileri çok sayıda küre içine yerleştirdiğimizde h≅r olacaktır.

o zaman 4.pi.h.r²/3≅4.pi.r.r²/3=4.pi.r³/3 olurki buda kürenin hacmini çok yaklaşık olarak verecektir.