Öncelikle aşağıdaki soruya açıklayıcı bi cevap alamadım 
Ayrıca f(x)=kökx g(x)=(xüssü4)+x+1 h(x)=2x-3 ise (f.g.h)'(1)=?
Ayrıca f(x)=kökx g(x)=(xüssü4)+x+1 h(x)=2x-3 ise (f.g.h)'(1)=?
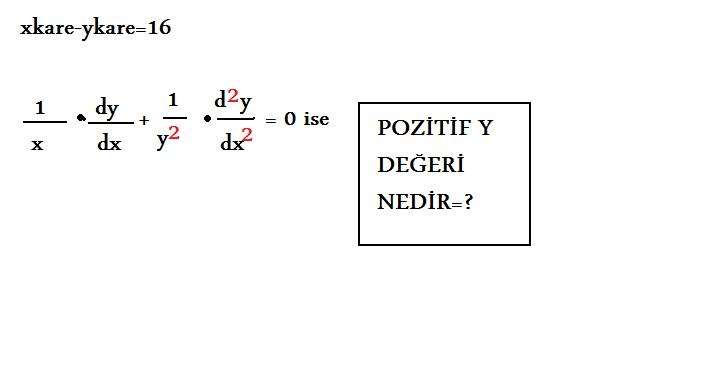
İlk soruda kapalı diferansiyelleme kullanalım:
x2-y2=16
2x-2y.y'=(16)'=0
-2y.y'=-2x
y'=x/y ise y'' ı bölme kuralı* ile bulabiliriz:
y' ı yerine yazarsak (y-x(x/y))/y2 elde ederiz. Bu da ((y²-x²)/y)/y²) 'ye eşittir.. Buradan da y''=(y²-x²)/y³ olur. Ayrıca y²-x²=-(x²-y²)=-16'dır. Yani y''=(-16)/y³ olur.
Daha sonra bulduğumuz değerleri soruda yerine yazalım:
olur.
Geri kalanı denklem çözme olduğundan geçiyorum, gerekirse açıklayabilirim.
*Bölme kuralı: (u/v)'=(u'v-uv')/v²
İyi günler.
x2-y2=16
2x-2y.y'=(16)'=0
-2y.y'=-2x
y'=
-2x
-2y
=
x
y
y'=x/y ise y'' ı bölme kuralı* ile bulabiliriz:
y''=
y-x.y'
y2
y' ı yerine yazarsak (y-x(x/y))/y2 elde ederiz. Bu da ((y²-x²)/y)/y²) 'ye eşittir.. Buradan da y''=(y²-x²)/y³ olur. Ayrıca y²-x²=-(x²-y²)=-16'dır. Yani y''=(-16)/y³ olur.
Daha sonra bulduğumuz değerleri soruda yerine yazalım:
1
x
x
y
+
1
y²
y²-x²
y³
elde ederiz. Buradan da
1
y
-
16
y⁵
olur.
Geri kalanı denklem çözme olduğundan geçiyorum, gerekirse açıklayabilirim.
*Bölme kuralı: (u/v)'=(u'v-uv')/v²
İyi günler.
Ayrıca f(x)=√x g(x)=x⁴+x+1 h(x)=2x-3 ise (f.g.h)'(1)=?
Çarpım kuralı kullanacağız. Önce kuralımıza bakalım:
(a.b.c)'=a'.b.c+a.b'.c+a.b.c'
Bu kurallar esnektir, istediğimiz kadar fonksiyon için genişletebiliriz.
Kuralda yerine yazmadan önce türevlerimizi hesaplayalım:
√x=x1/2 ise (√x)' = 1/2(x-1/2)=1/2(1/√x) olur.
(x⁴+x+1)'=4x³+1
(2x-3)'=2
Bunları yerine yazarsak;
elde ederiz. Burada işlemleri yapabiliriz; ama x yerine 1 yazıp çözebiliriz.
İyi günler.
Çarpım kuralı kullanacağız. Önce kuralımıza bakalım:
(a.b.c)'=a'.b.c+a.b'.c+a.b.c'
Bu kurallar esnektir, istediğimiz kadar fonksiyon için genişletebiliriz.
Kuralda yerine yazmadan önce türevlerimizi hesaplayalım:
√x=x1/2 ise (√x)' = 1/2(x-1/2)=1/2(1/√x) olur.
(x⁴+x+1)'=4x³+1
(2x-3)'=2
Bunları yerine yazarsak;
1
2√x
(x⁴+x+1).(2x-3)+√x.(4x³+1).(2x-3)+√x.(x⁴+x+1).(2)
elde ederiz. Burada işlemleri yapabiliriz; ama x yerine 1 yazıp çözebiliriz.
İyi günler.
x2-y2=16
2x-2y.y'=(16)'=0 burda yaptığının işlemde neyin türevini alıyosun?
2x-2y.y'=(16)'=0 burda yaptığının işlemde neyin türevini alıyosun?
Kapalı diferansiyelleme(implicit differentiation) yapılıyor. Elimizde eşitlik varsa her terimin tek tek türevini alabiliriz, bu sayede eşitlik bozulmaz.
Orada x², y² ve 16'nın türevlerini tek tek aldım. Türevler x'e göre olduğu için bağımlı değişken olan y'nin türevi bir de y' ile çarpılıyor.
İyi günler.
Orada x², y² ve 16'nın türevlerini tek tek aldım. Türevler x'e göre olduğu için bağımlı değişken olan y'nin türevi bir de y' ile çarpılıyor.
İyi günler.
. Türevler x'e göre olduğu için bağımlı değişken olan y'nin türevi bir de y' ile çarpılıyor. bunu anlamadım 
Fonksiyonumuzu düzenleyelim:
x²-y²=16
x²-16=y²
±√x²-16=y oldu.
Burada y'nin değeri x'in değerine göre değişir, dolayısıyla y'ye bağımlı değişken diyoruz.
Kapalı diferansiyellemede bağımlı değişkenler önce bağımsızmış gbi türevleri alınır, daha sonra kendisinin türevi ile çarpılır.
y=x²+y gibi bir örnek düşünelim:
dy/dx=(x²)'+(y)' dir. x'e göre türev aldığımızdan x²'nin türevini rahatlıkla alabiliriz. Daha sonra y'yi sanki bağımsız değişkenmiş gibi türevini alıp, kendisinin türevi ile çarparız:
dy/dx=2+1.y' olur.
İyi günler.
x²-y²=16
x²-16=y²
±√x²-16=y oldu.
Burada y'nin değeri x'in değerine göre değişir, dolayısıyla y'ye bağımlı değişken diyoruz.
Kapalı diferansiyellemede bağımlı değişkenler önce bağımsızmış gbi türevleri alınır, daha sonra kendisinin türevi ile çarpılır.
y=x²+y gibi bir örnek düşünelim:
dy/dx=(x²)'+(y)' dir. x'e göre türev aldığımızdan x²'nin türevini rahatlıkla alabiliriz. Daha sonra y'yi sanki bağımsız değişkenmiş gibi türevini alıp, kendisinin türevi ile çarparız:
dy/dx=2+1.y' olur.
İyi günler.
