
Bugün buradaki (cember uzunluk soruları) diğer konunuzda cevaplanmıştır. Bu konu yarına kadar kapalıdır. Bu konu cevaplanana kadar soru göndermeyiniz.
C-1) Bu soruda buradaki (11.sınıf cember uzunluk soruları) konudaki 3. sorudur. Çözülmüştür.
C-3)Yukarıdan aşağı 3. soru.
Büyük çemberin yarıçapı r olsun. O₁ O₂ B noktallarını birleştirirsek |O₁O₂|=r-5 ayrıca |O₁F|=r-6 dir. O₁FO₂ üçgeni dik üçgen olduğu açıktır.
5, r-6 ve hipotenüs r-5 olan bir dik üçgende pisagor yazılırsa r=18 çıkar.
|O₁F|=r-6=18-6=12
Küçük çembere teğetlikten |ED|=|EF| dir.
|ED|=|O₁F|+r=12+18=30=|EF|
C-4)Yukarıdan aşağı 4. soru.
Teğteler dörtgeninde

yazılan bölümlerdeki uzunluklar birbirine eşittir.
Dik üçgenden |AD|=10=a+b ve |BC|=12=c+d
istenen |AB|=|DC|=a+d=b+c dir.
a+b+c+d=10+12=22 dir. a+d=b+c için 22/2=11=a+d=b+c dir. istenen 11
C-5)

O merkezinden F, E ve D noktalarına yarıçap çizilirse OD ve OE 5 verilmiş. DE de 5 verilmiş . DOE üçgeni eşkenar üçgendir. FLE ve DME yayları eşit olunca FOE açısı ile DOE eşit 60 olmalıdır. F noktasındaki teğetlikten 90 dır. EOFC dörtgenindeki açılardan C açısına 90 derece kaldığı görülür.
C-6) Teğteliklerden A açısının 90 olduğu açıktır. CAd üçgeni 3,4,5 üçgeni olur. ACBD dörtgeni düşünüldüğünde BU örtgen deltoittir. Deltoitte köeşegenler dik kesişir. Yani AB ile CD dik keşişir. CAD üçgeninde AB doğru parçasının bir kısmı yüksekliktir. Burada öklidden üçgenin tüm parçları bulursa AB nini yarısı olan yükseklik 2,4 Ab ise 4,8 çıkar.
C-3)Yukarıdan aşağı 3. soru.
Büyük çemberin yarıçapı r olsun. O₁ O₂ B noktallarını birleştirirsek |O₁O₂|=r-5 ayrıca |O₁F|=r-6 dir. O₁FO₂ üçgeni dik üçgen olduğu açıktır.
5, r-6 ve hipotenüs r-5 olan bir dik üçgende pisagor yazılırsa r=18 çıkar.
|O₁F|=r-6=18-6=12
Küçük çembere teğetlikten |ED|=|EF| dir.
|ED|=|O₁F|+r=12+18=30=|EF|
C-4)Yukarıdan aşağı 4. soru.
Teğteler dörtgeninde

yazılan bölümlerdeki uzunluklar birbirine eşittir.
Dik üçgenden |AD|=10=a+b ve |BC|=12=c+d
istenen |AB|=|DC|=a+d=b+c dir.
a+b+c+d=10+12=22 dir. a+d=b+c için 22/2=11=a+d=b+c dir. istenen 11
C-5)
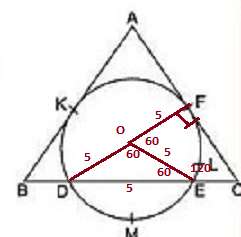
O merkezinden F, E ve D noktalarına yarıçap çizilirse OD ve OE 5 verilmiş. DE de 5 verilmiş . DOE üçgeni eşkenar üçgendir. FLE ve DME yayları eşit olunca FOE açısı ile DOE eşit 60 olmalıdır. F noktasındaki teğetlikten 90 dır. EOFC dörtgenindeki açılardan C açısına 90 derece kaldığı görülür.
C-6) Teğteliklerden A açısının 90 olduğu açıktır. CAd üçgeni 3,4,5 üçgeni olur. ACBD dörtgeni düşünüldüğünde BU örtgen deltoittir. Deltoitte köeşegenler dik kesişir. Yani AB ile CD dik keşişir. CAD üçgeninde AB doğru parçasının bir kısmı yüksekliktir. Burada öklidden üçgenin tüm parçları bulursa AB nini yarısı olan yükseklik 2,4 Ab ise 4,8 çıkar.
Arkadaşlar, 2. soruda merkezlerin dik üçgen oluşturacağına nasıl bir mazeret getirebiliriz. 5,12 üçgeni var ama dik olduğunu açıklamamız lazım.
dila94, ziyaretçilere bundan sonra 3 soru sorma hakkı getirdik. Buna dikkat ediniz bundan sonra.
dila94, ziyaretçilere bundan sonra 3 soru sorma hakkı getirdik. Buna dikkat ediniz bundan sonra.
bence dik olmaz zorunda değil, ve bu yüzden soru bu haliyle çözümsüz kalır.
Diğer çözümlü sorular alttadır.
.11. sınıf Çember Daire Soruları Çember ile İlgili Çözümlü Sorular Çemberde Kuvvet ile İlgili Çözümlü Sorular Çemberde Uzunluk Çözümlü Sorular
Tüm Etiketler
Tüm Etiketler
