10. soruyu 5,6 defa çözdüm hepsinde de 4/5 cevabını buluyorum nerde hata yapıyorum bir türlü çözemedim.
4) Bir geometrik dizinin ilk terimi a, ortak çarpanı 2, n. terimi b dir. Bu dizinin ilk n terimi toplamı?
a)b-2a b) b+a-1 c)2b-a d)b-a e)b-a+1
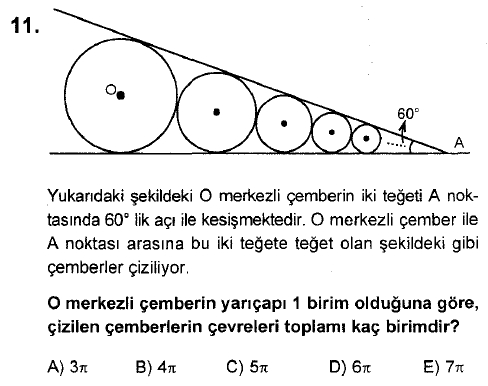
Bu sorularımda yardımcı olabilirseniz minnettar olurum.
Şimdiden teşekkürler
cevap 10.
a₁=> k=3 için, (2/3)^2=4/9, r=2/3
a₁/(1-r)=(4/9)/(1-(2/3))=4/3
cevap 4.
a₁=a, r=2
a_n=a₁.r^(n-1)=a.2^(n-1)=b verilmiş, (2^n)/2=b/a, 2^n=2b/a)
ilk n terim toplamı: a₁.(1-r^n)/(1-r)=a.(1-2^n)/(-1)=a.(1-(2b/a)/-1=2b-a
a₁=> k=3 için, (2/3)^2=4/9, r=2/3
a₁/(1-r)=(4/9)/(1-(2/3))=4/3
cevap 4.
a₁=a, r=2
a_n=a₁.r^(n-1)=a.2^(n-1)=b verilmiş, (2^n)/2=b/a, 2^n=2b/a)
ilk n terim toplamı: a₁.(1-r^n)/(1-r)=a.(1-2^n)/(-1)=a.(1-(2b/a)/-1=2b-a
:s
cevap 2.
ifadenin önünde n'e bağlı bir sayı varsa formül a₁/(1-r) değil de a₁/(1-r)² oluyordu.
n.2/(2^n)=2n.(1/2)^n, r=1/2, a₁=> n=1 için: 1/2
a₁/(1-r)²=(2.1).(1/2)/((1-(1/2)²)=4
cevap 6. f(x)=(n-1)³, f(x+1)=225
f(x+1)= toplam sembolü ile n=2'den (x+1)'e (n-1-1)³=225
0³+1³+2³+.........+(x+1-2)³=225
[(x-1).(x-1+1)/2]²=15²
(x-1).x=30, x=6
cevap 2.
ifadenin önünde n'e bağlı bir sayı varsa formül a₁/(1-r) değil de a₁/(1-r)² oluyordu.
n.2/(2^n)=2n.(1/2)^n, r=1/2, a₁=> n=1 için: 1/2
a₁/(1-r)²=(2.1).(1/2)/((1-(1/2)²)=4
cevap 6. f(x)=(n-1)³, f(x+1)=225
f(x+1)= toplam sembolü ile n=2'den (x+1)'e (n-1-1)³=225
0³+1³+2³+.........+(x+1-2)³=225
[(x-1).(x-1+1)/2]²=15²
(x-1).x=30, x=6
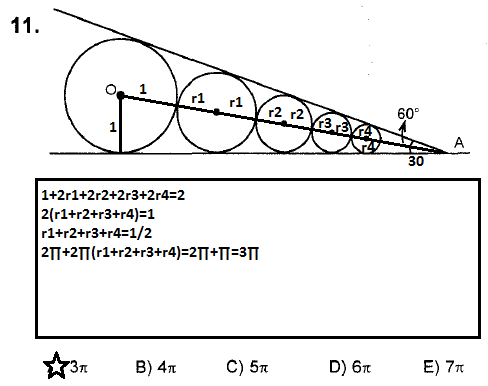
bizim bu çemberler sonsuza gitmiyor muydu yahu?
Sonsuza gidip ne yapacaklar ki Sonsuza kim gitmiş de geri dönmüş Bunlar yol yakınken dönelim demişler
Sonsuza kim gitmiş de geri dönmüş Bunlar yol yakınken dönelim demişler Sonsuza gidip ne yapacaklar ki Sonsuza kim gitmiş de geri dönmüş Bunlar yol yakınken dönelim demişler
Sonsuza kim gitmiş de geri dönmüş Bunlar yol yakınken dönelim demişler 
Haklısın fark etmemişim. Fakat çok bir şey değişmiyor.
r1+r2+r3+r4 dediğim kısım yerine;
r1+r2+r3+r4+r5+r6+..... şeklinde sonsuza giden bir toplam yazarız. Bu toplamın sonucu 1/2'ye eşittir. Çemberin çevresi formülünde parantez içine alırsak yine aynı sonuç çıkar.
r1+r2+r3+r4 dediğim kısım yerine;
r1+r2+r3+r4+r5+r6+..... şeklinde sonsuza giden bir toplam yazarız. Bu toplamın sonucu 1/2'ye eşittir. Çemberin çevresi formülünde parantez içine alırsak yine aynı sonuç çıkar.
Evet çözümleriniz için teşekkür ederim fakat 10. soru ile ilgili anlayamadığım birşey var onu sormak istiyorum sizlere.
r nin neden 2/3 olduğunu anlamadım. İlk terim 4/9 2. terim 4/9 un karesi, bu durumda r=4/9 olmaz mı çözümü yukarıdaki gibi yaptım ancak neden yanlış olduğunu anlayamıyorum. Please help
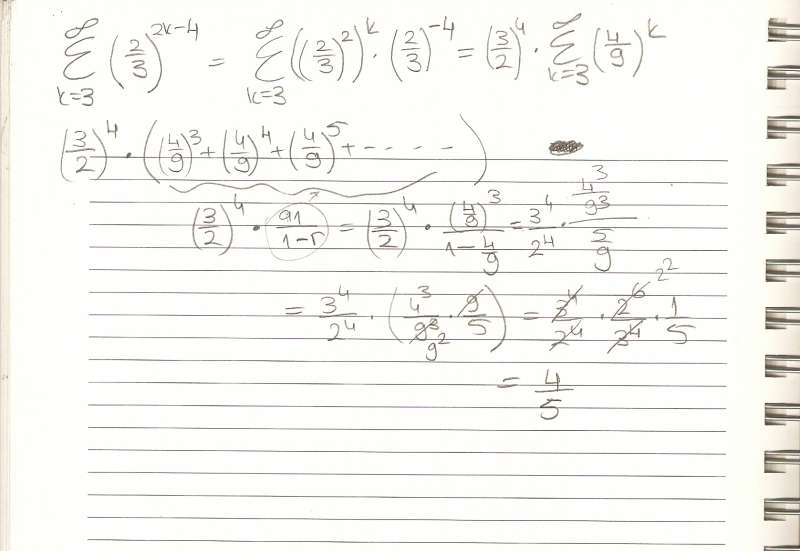
r nin neden 2/3 olduğunu anlamadım. İlk terim 4/9 2. terim 4/9 un karesi, bu durumda r=4/9 olmaz mı çözümü yukarıdaki gibi yaptım ancak neden yanlış olduğunu anlayamıyorum. Please help
Haklısınız, yalnız bir nokta var: r'yi en sade haliyle almalısınız. Yani (2/3)^2^k alınca r=4/9 oluyor. Fakat (2/3)^k^2 şeklinde aldığımızda, k üssüne bağlı en sade değeri almış olursunuz.
Diğer çözümlü sorular alttadır.