1)

2)

3)

4)

5)


2)

3)

4)

5)

C-5)

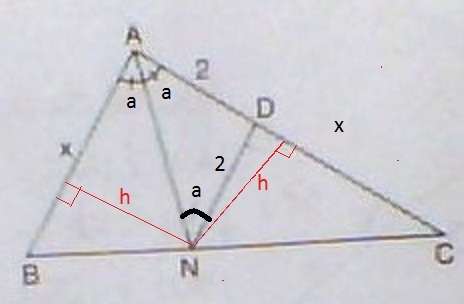
Paralellikten A(AND)=a olacaktır.
|DN|=2 olacaktır.
Açıortay doğrusu üzerinden kenarlara inilen dikmeler eşittir. ANB ile DNC üçgenlerin yükseklikleri eşit olacaktır. Alanları da eşitse Tabanları eşit olacaktır. |DC|=x olacaktır.
Şimdi paralellikten benzerlik yazarsak
Bu denklemi çözersek x=√5 + 1 çıkar.
Paralellikten A(AND)=a olacaktır.
|DN|=2 olacaktır.
Açıortay doğrusu üzerinden kenarlara inilen dikmeler eşittir. ANB ile DNC üçgenlerin yükseklikleri eşit olacaktır. Alanları da eşitse Tabanları eşit olacaktır. |DC|=x olacaktır.
Şimdi paralellikten benzerlik yazarsak
x
x+2
=
2
x
Bu denklemi çözersek x=√5 + 1 çıkar.
C-4)

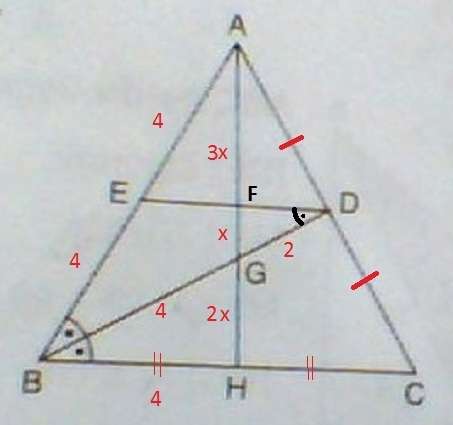
G ağırlık merkezi ve [BD] G noktasından geçtiği için kenar ortaydır (hemde açıortaydı).
|AD|=|DC| ve [AH] da G den geçtiği için |BH|=|HC| dir
[ED] nin paralelliğinden EDB açısıda noktalı açıya eşit olacaktır. |ED|=4=|EB| dir.
[ED] nin [BC]'ye paralelliğinden |AD|=|DC| eşit olduğundan |BC|=2.|ED|=2.4=8 dir ve |BH|=4
[ED] nin [BC]'ye paralelliğinden |AD|=|DC| eşit olduğundan |EB|=4=|AE|
Yine benzer durumlardan dolayı |AF|=3x ise |FH|=3x ve G ağırlık merkezi olduğundan |AG| nin |GH| nin 2 katı olması için |FG|=x ve |GH|=2x olmalıdır.
|BD|=6 ise Agırlık merkezinden dolayı |BG|=4 ve |GD|=2 dir.
ABH üçgeninde açıortay formülü yazılırsa
4²= 4.8 − 2x.4x
x=√2
|AH|=6√2
G ağırlık merkezi ve [BD] G noktasından geçtiği için kenar ortaydır (hemde açıortaydı).
|AD|=|DC| ve [AH] da G den geçtiği için |BH|=|HC| dir
[ED] nin paralelliğinden EDB açısıda noktalı açıya eşit olacaktır. |ED|=4=|EB| dir.
[ED] nin [BC]'ye paralelliğinden |AD|=|DC| eşit olduğundan |BC|=2.|ED|=2.4=8 dir ve |BH|=4
[ED] nin [BC]'ye paralelliğinden |AD|=|DC| eşit olduğundan |EB|=4=|AE|
Yine benzer durumlardan dolayı |AF|=3x ise |FH|=3x ve G ağırlık merkezi olduğundan |AG| nin |GH| nin 2 katı olması için |FG|=x ve |GH|=2x olmalıdır.
|BD|=6 ise Agırlık merkezinden dolayı |BG|=4 ve |GD|=2 dir.
ABH üçgeninde açıortay formülü yazılırsa
4²= 4.8 − 2x.4x
x=√2
|AH|=6√2
Çok teşekkürler hocam emeğinize sağlık. Diğer soruları da çözerseniz daha da müteşekkir olacağım.
C-3)

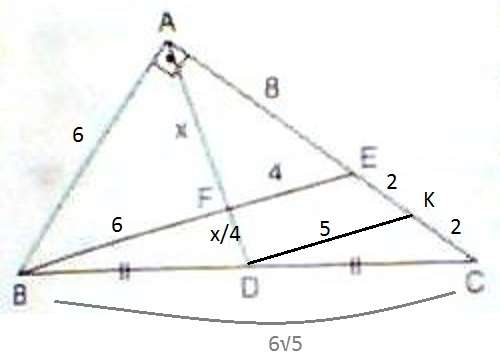
[BE]'ye paralel olacak şekilde [DK] çizilirse |CD|=|DB| olduğu için |CK|=|KE|=2
oranından |BE|=10 çıkar. BAE dik üçgeninden |AB|=6 çıkar. BAE dik üçgeninden |BC|=6√5 çıkar.
|AD|= |BD|/2 den
x+(x/4)=3√5
x=12√5/5=12/√5
Not: Diğerlerine akşam uğraşacağım.
[BE]'ye paralel olacak şekilde [DK] çizilirse |CD|=|DB| olduğu için |CK|=|KE|=2
|AE|
|AK|
=
|FE|
|DK|
=
|AF|
|AD|
oranından |DK|=5 çıkar ve |FD|=x/4
|CK|
|CE|
=
|DK|
|BE|
oranından |BE|=10 çıkar. BAE dik üçgeninden |AB|=6 çıkar. BAE dik üçgeninden |BC|=6√5 çıkar.
|AD|= |BD|/2 den
x+(x/4)=3√5
x=12√5/5=12/√5
Not: Diğerlerine akşam uğraşacağım.
C-2)

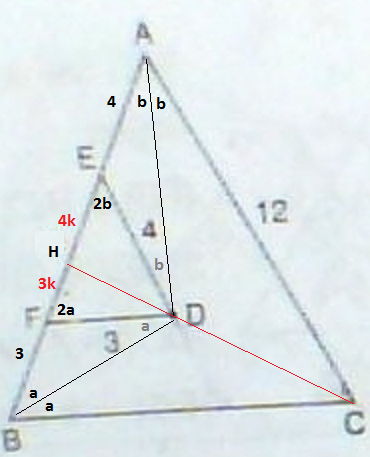
DA ve DB leri çizdiğimizde D noktası açırortay olduğundan A açısı b ile b ve B açısı a ile a alarak adlandırabileceğiz.
Paralelliklerden E açısı 2b ve F açısı 2a olacaktır. O zaman EDA açısı b ve FDB açısı a olmalıdır. O zaman EA=4 ve FB=3 olmalıdır.
CH açıortaydır FD=3 ise FH=3k ve DE=4 ise HE=4k diyebiliriz (açıortay özelliğinden).
ED/AC=HE/HA
Buradan 4k=2 ve k=1/2 dir. x=7k=7.(1/2)=3,5
DA ve DB leri çizdiğimizde D noktası açırortay olduğundan A açısı b ile b ve B açısı a ile a alarak adlandırabileceğiz.
Paralelliklerden E açısı 2b ve F açısı 2a olacaktır. O zaman EDA açısı b ve FDB açısı a olmalıdır. O zaman EA=4 ve FB=3 olmalıdır.
CH açıortaydır FD=3 ise FH=3k ve DE=4 ise HE=4k diyebiliriz (açıortay özelliğinden).
ED/AC=HE/HA
Buradan 4k=2 ve k=1/2 dir. x=7k=7.(1/2)=3,5
Emeğinize sağlık hocam tekrar teşekkür ediyorum size. 1. soruyu da uygun bir vaktinizde çözmeniz temennisiyle.
Güncel.
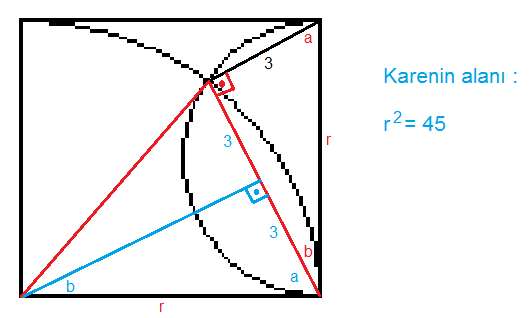
Önce kırmızıları takip edin sonra mavileri. Anlaşılmayan bir yer olursa kelimelerle ifade etmeye çalışayım.
Anladım teşekkürler emeğinize sağlık. Bu türlü hiç düşünmemiştim. Teğetlerle boğuşmuştum açıkçası 
