Sorular klasik olduğu için şık veremiyorum..
1)
x²-9x²-x-20
≤0 eşitsizliğini sağlayan x tamsayılarının toplamı kaçtır?
2)
3Л/2<0<2Л olmak üzere, cotѲ=-3 olduğuna göre
sinѲ+cosѲ6.tanѲ
ifadesinin değeri kaçtır?
3)y=x²-2ax+b parabolünün tepe noktası T(-1,2) olduğuna göre, a+b toplamı kaçtır?
4)

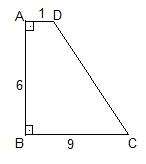
ABCD dik yamuk, [AD]┴[AB] , [AB]┴[BC] |AD|=1cm , |AB|=6 cm , |BC|=9 cm old. göre sin(DĈB) nin değeri kaçtır?
5)
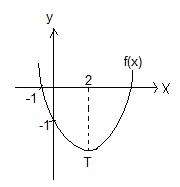
Yukarıdaki parabol f(x)=ax²+bx+c fonksiyonunun grafiğidir. Buna göre, a+b+c kaçtır?
Şimdiden teşekkürler..